沖合洋上建設工事における起重機船動揺低減対策実証試験
白島石油備蓄株式会社
建設一部次長
建設一部次長
鍛 治 壮 吉
ハザマ 九州支店土木部
宮 本 好 英
ハザマ 土木統括本部
技術設計第二部
技術設計第二部
桑 原 正 博
飛島建設株式会社
九州支店土木部
九州支店土木部
松 尾 和 男
1 はじめに
沖合洋上における起重機船の動揺低減すなわち稼働率の向上は,沖合人工島等の洋上構造物の建設技術の向上に大きく寄与するものである。
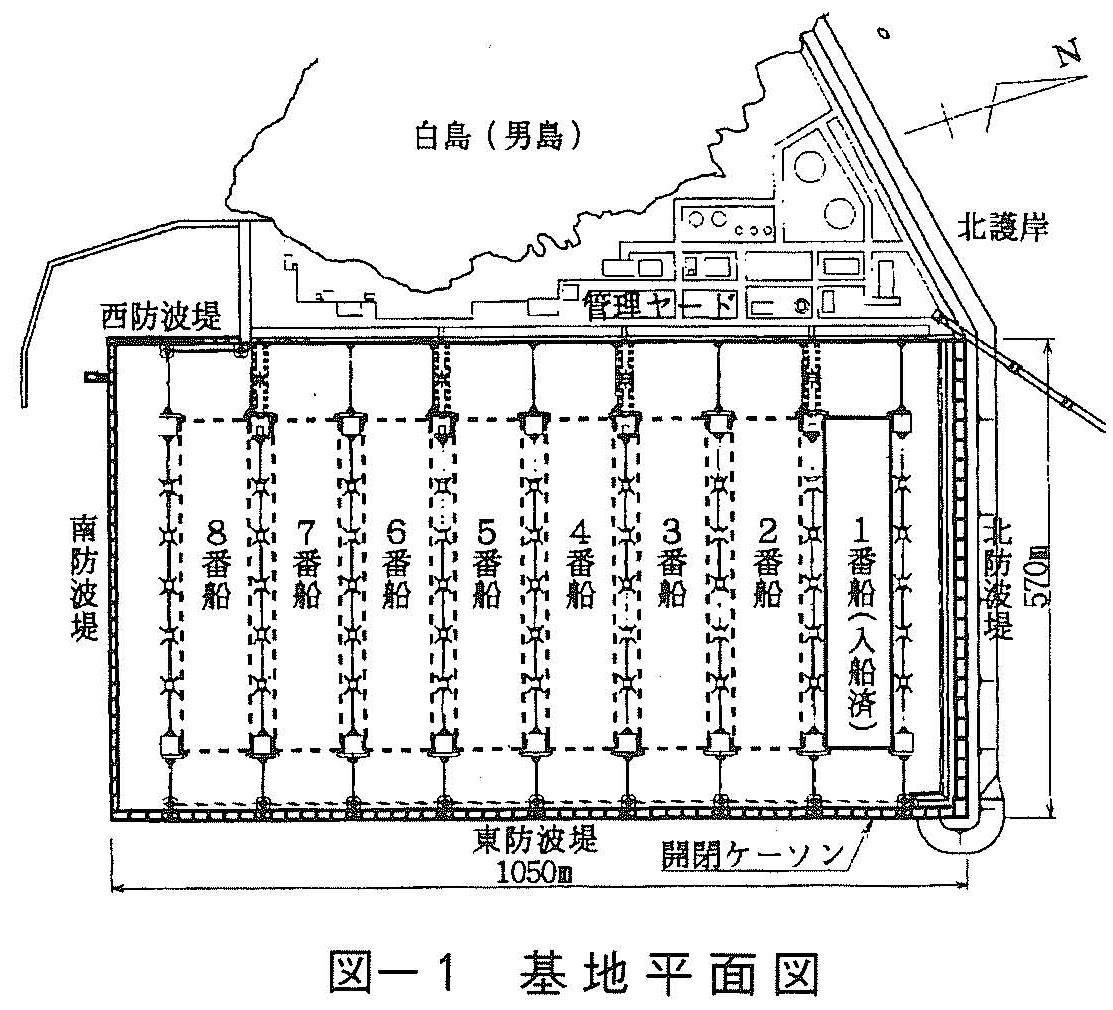
白島石油備蓄基地建設工事では,原油貯蔵船を防波堤で囲まれた基地内に入船させる(図ー1)。この際,入口となる東防波堤を開口する必要があり,大型起重機船(3,000t級)を用いて貯蔵船前面の開閉ケーソン(幅11.5m,長さ18.5m,高さ15.5m,吊上重量約2,000t,吊点40箇所)を1函ずつ合計5函を吊上移動する(図ー2)。
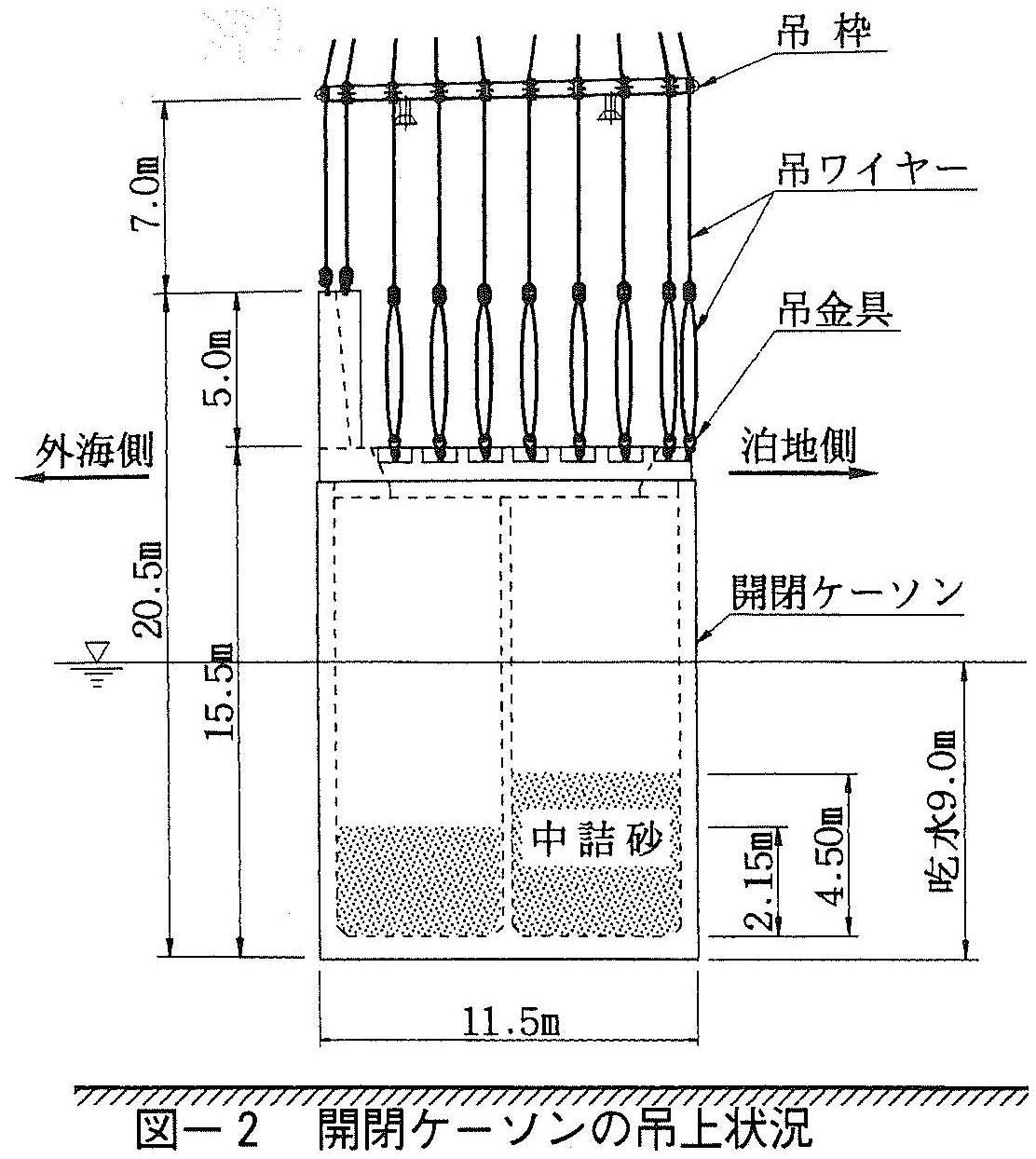
吊上作業に用いる吊ワイヤーは直径100mm(単位重量36kg/m)で,ワイヤー先端には重量約130kgの吊金具が吊点1箇所につき1個ずつ設置されている。開閉ケーソンを吊上げるため,人力作業により吊金具をケーソンの吊筋へ連結(玉掛け)するが,吊枠下のワイヤー・吊金具だけでも,吊点1箇所当たりの取扱い重量は,パラペット位置で約380kg,本体上部工位置で約560kgとなる(図ー2参照)。
吊上作業は泊地外側から行わざるを得ないので,起重機船が波浪の影響を受けワイヤー先端の動揺量が大きくなると,吊金具を開閉ケーソンの吊筋へ連結(玉掛け)する際,ワイヤー先端(吊金具)の動揺により作業員が負傷あるいは海中に突き落とされる等の危険が生じ,玉掛け作業が不可能となる。
このため,過去の経験からケーソン開閉工事における起重機船の作業限界条件として,有義波高0.5m,有義波周期6.0秒を設定している。
本工事では,平成8年度の完工までに8隻の入船を予定しており,今後起重機船の稼働率向上が望まれる。この一方で,平成6年度の貯蔵船入船工事(2番船入船)を3ヶ月後に迎えようとしていた。このため,実施が比較的容易で即時対応が可能と考えられる起重機船ジブの倒伏および起重機船バラストタンク内への海水バラスト追加投入(海水バラスト増量)による起重機船の動揺低減効果を確認するため,現地海域で玉掛け直前を想定した実証試験を行った。
本文は,この実験結果と,2番船入船時における対策適用結果について整理したものである。
なお,起重機船作業については,現地作業が可能な波浪条件になるまで起重機船を避泊地で待機させておくのが現状であり,船体自身の稼働率を向上させるための対策について,検討した事例がないことをはじめに述べておく。
2 実験方法
(1)実験ケース
実験では,玉掛け直前の状態,すなわち,吊ワイヤーがケーソンに連結されていない状態のもと,起重機船の動揺によって吊枠および吊ワイヤー等に生じる動揺量を計測した。実験に用いた起重機船の仕様を図ー3に示す。
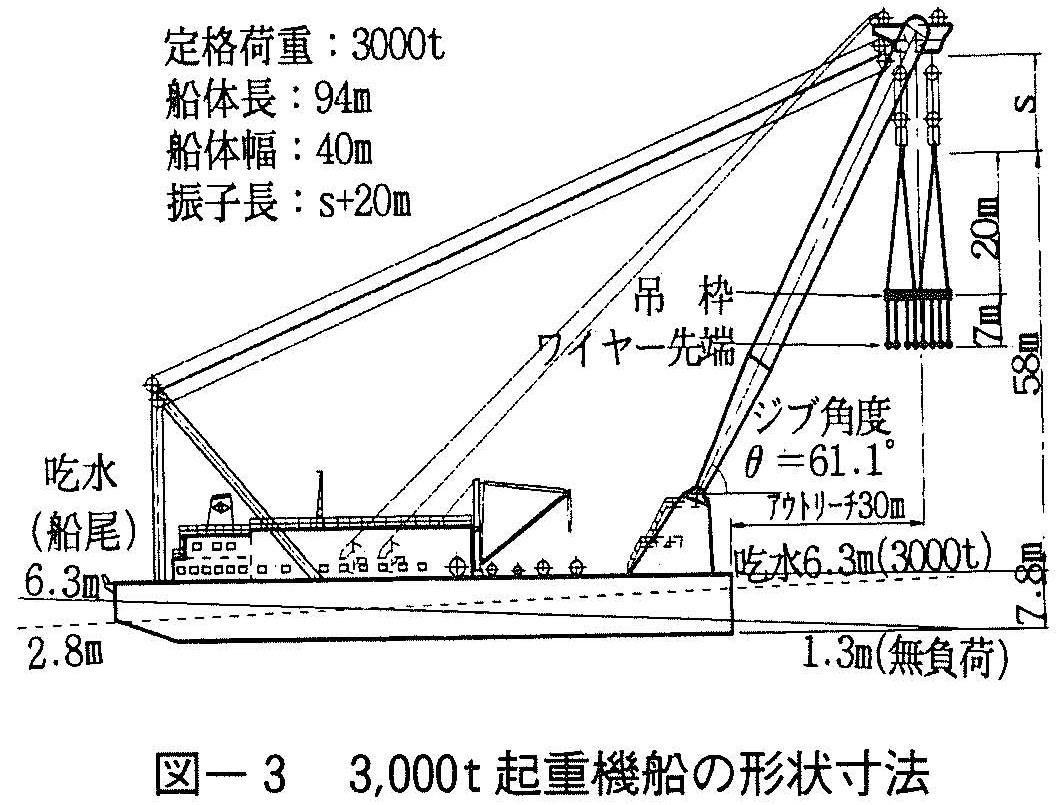
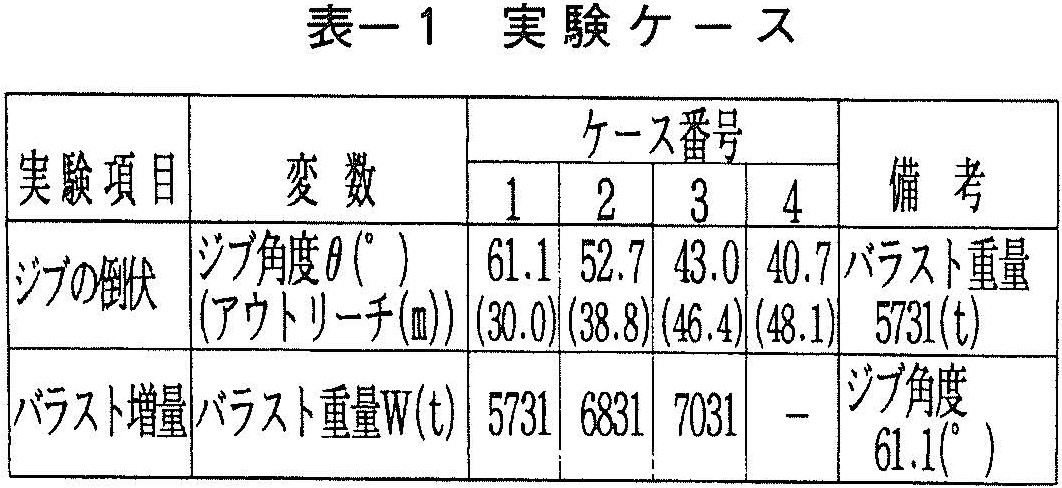
実験ケースの概要は以下のとおり(表ー1参照)。
・起重機船ジブの倒伏:ジブ先端の高さを低くし,船体動揺に対するジブ先端の動揺低減効果を期待するもので,バラスト重量を5731tに固定し,ジブ角度θを61.1゜から40.7°(2000t吊上可能なジブ角度)まで変化させた実験を行った。
・海水バラストの増量:海水バラストを追加投入して吃水を増し,揺れに対する復元性の向上効果を期待するもので,ジブ角度を61.1゜に固定し,バラスト重量Wを5731tから7031t(2000t吊上可能なバラスト重量)に変化させた実験を行った。
(2)計測項目および計測方法
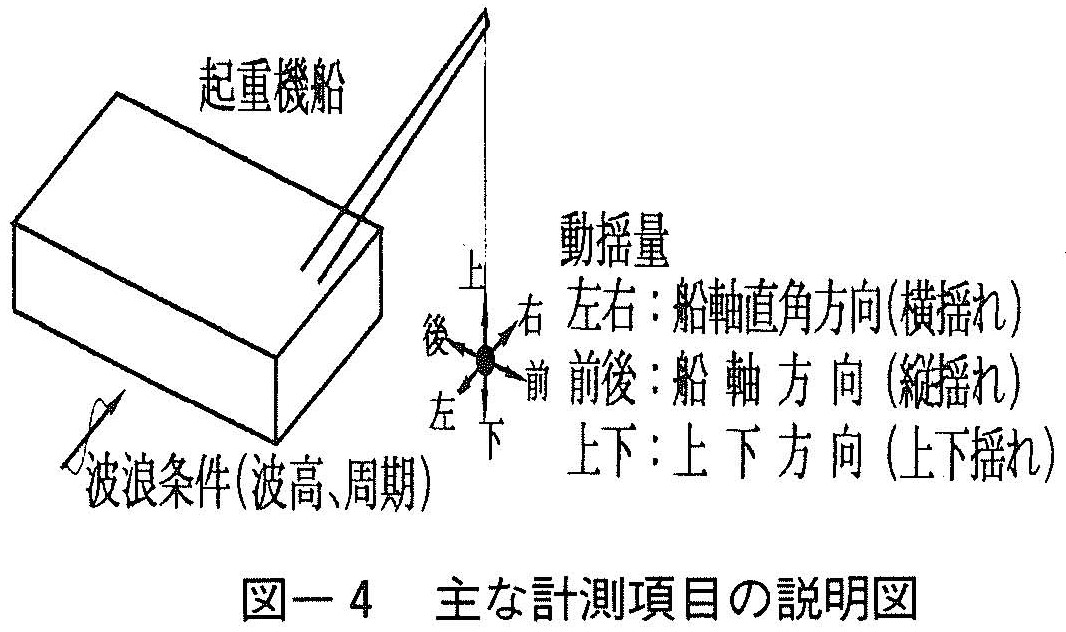
主要計測項目は波浪条件と動揺量である(図ー4)。
波浪条件は基地北側に位置する定点観測施設で観測されているが,船体付近での波浪観測も実施した。
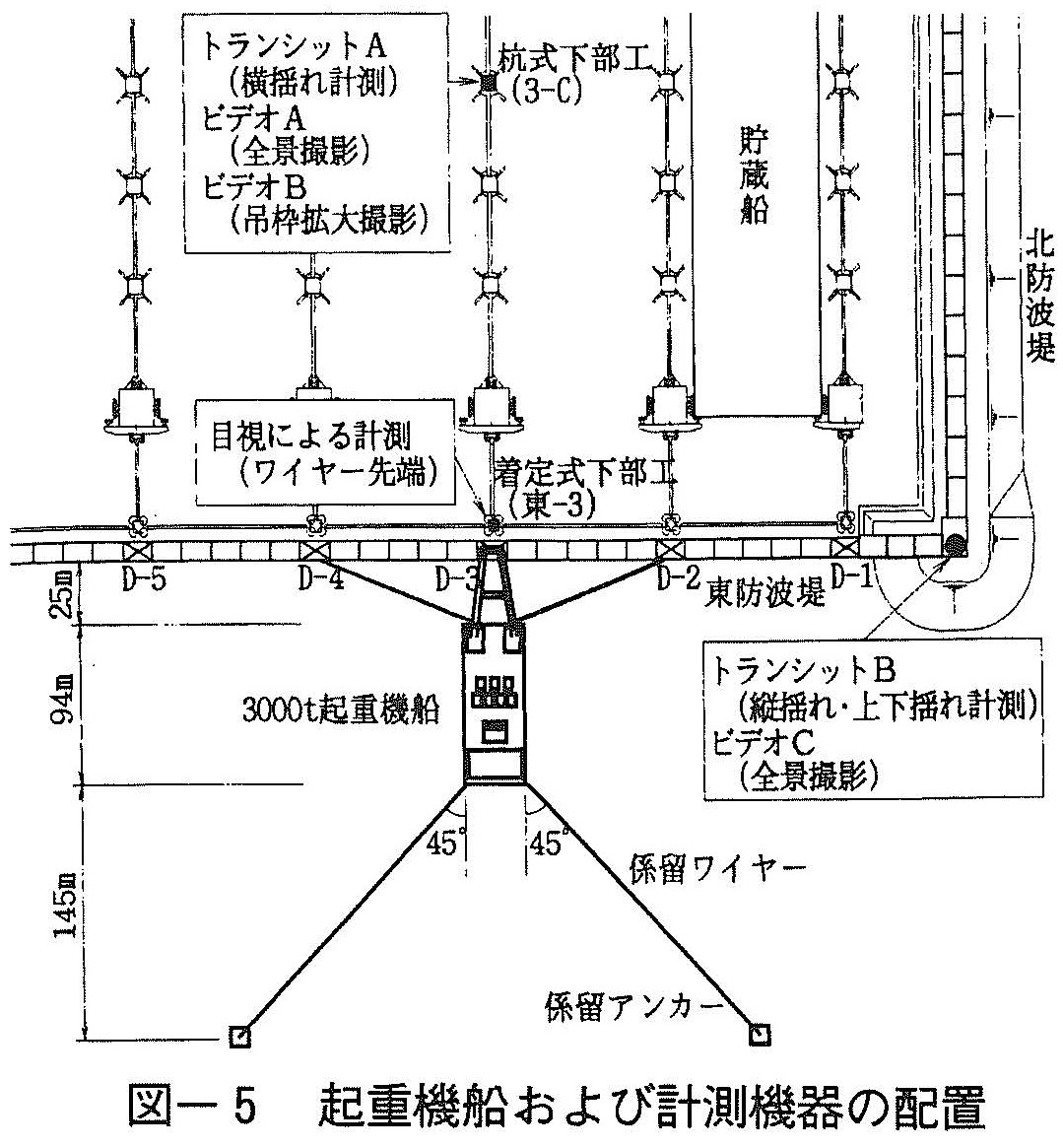
動揺量については,船軸直角方向(横揺れ),船軸方向(縦揺れ),上下方向(上下揺れ)を対象に,ジブ先端,吊枠およびワイヤー先端に目盛板を設置して,トランシットとVTR撮影による計測を実現した(図ー5)。
また,動揺周期については,ジブ先端と吊枠について,VTRからそれぞれ動揺変位が極大から次の極大になるまでの時間を各実験ケースにつき約10回計測し,その平均値を算定することとした。
3 実験結果
(1)船体および吊枠の動揺周期
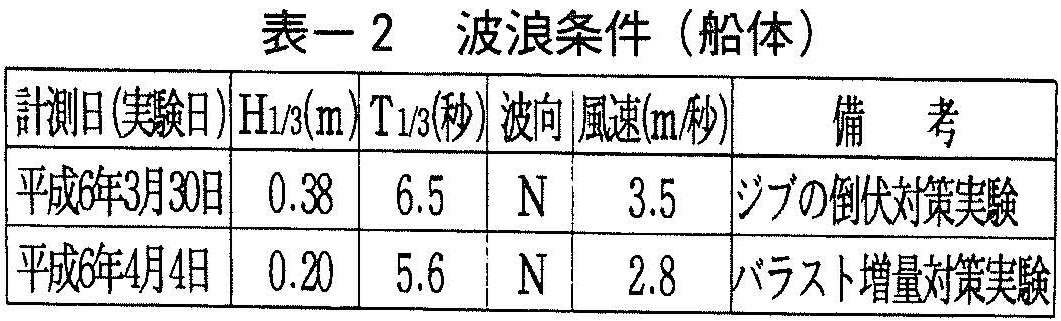
表ー2に現地波浪条件(船体付近)の観測結果を示す。
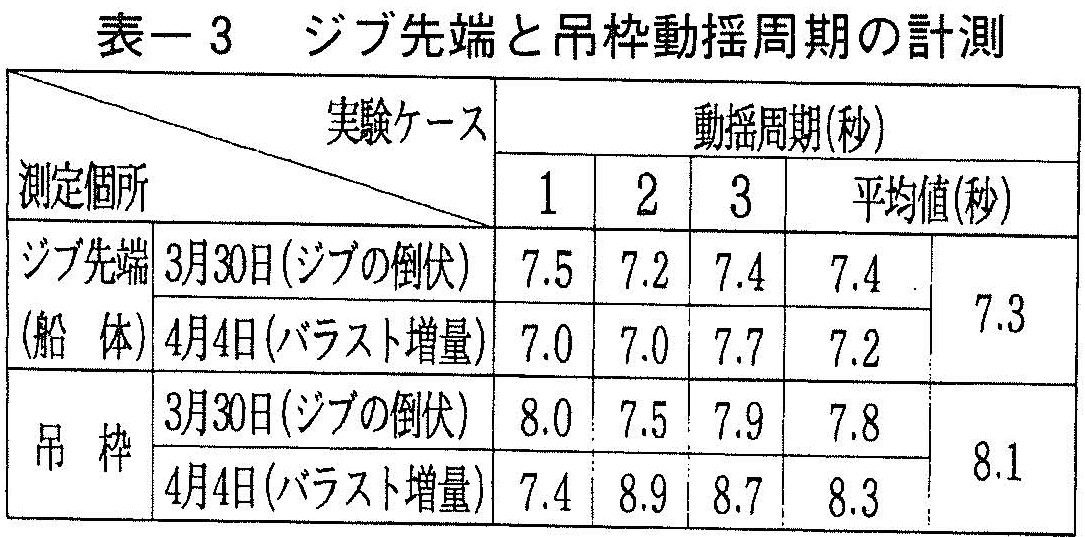
また,ビデオBから得られたジブ先端と吊枠の横揺れ動揺周期の計測結果を表ー3に示す。なお,ジブは船体に剛結されているので,ジブ先端の動揺周期は船体動揺周期に等しいものとする。
a)船体の動揺周期
表ー3より,船体の動揺周期の平均値は,3月30日が7.4秒,4月4日が7.2秒でほぼ等しく(有意水準5%による平均値の検定結果から有意差が認められなかった1)),両日の平均値は7.3秒となった。
これに対して,波の周期は,3月30日が約6.5秒,4月4日が約5.6秒であり,現地水深が約25mなので,相対水深はそれぞれ0.39,0.51となる。したがって,4月4日の場合は深海波の条件2)に近く,3月30日と4月4日とでは波浪の性質が異なると考えられるが,船体動揺周期に有意差が認められなかったので,実験範囲(有義波周期5.6~6.5秒)では,波の周期が船体動揺周期に与える影響は小さいものと考えられる。
b)吊枠の動揺周期
吊枠動揺周期の平均値は3月30日が7.8秒,4月4日が8.3秒であり,船体動揺周期と同様に両日で有意差がみられず,両日の平均値は約8.1秒であった。
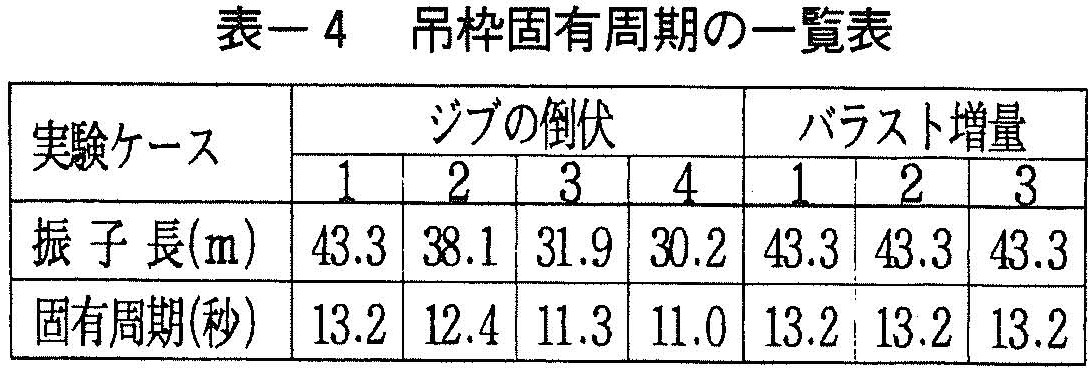
一方,吊枠の固有周期は,振子長によって決まる(表ー4)が,吊枠動揺周期は吊枠固有周期と異なり,船体動揺周期に近いので,吊枠は支点(ジブ先端)に生じる動揺の影響を受けているものと考えられる。
(2)各計測位置別の動揺量
a)動揺量の範囲と平均値
動揺量測定値が正規分布に従うものと仮定すると,個々の測定値δが取り得る範囲は,平均値δaveと標本標準偏差σn-1により,次式で表される1)。
δave - R/2 ≦ δ ≦ δave + R/2 ………(1)
ただし,R:範囲(最大値と最小値の差)で,
R/2=u(α)・σn-1
u(α):包含確率αにより決まる定数
包含確率を99%(u(0.01)=2.5758)として,各ケース別の実験結果とともに範囲推定値を表ー5に示す。
例えば,ジブの倒伏実験ケース1のジブ先端の動揺量範囲推定値は0.08m~0.64mと計算されるが,測定値は最小値0.19m,最大値0.56mであり,計算で求めた動揺量範囲内の値となっている。
他の実験ケースについても同様であり,測定値は,正規分布を仮定した99%範囲内にほぼ含まれる。
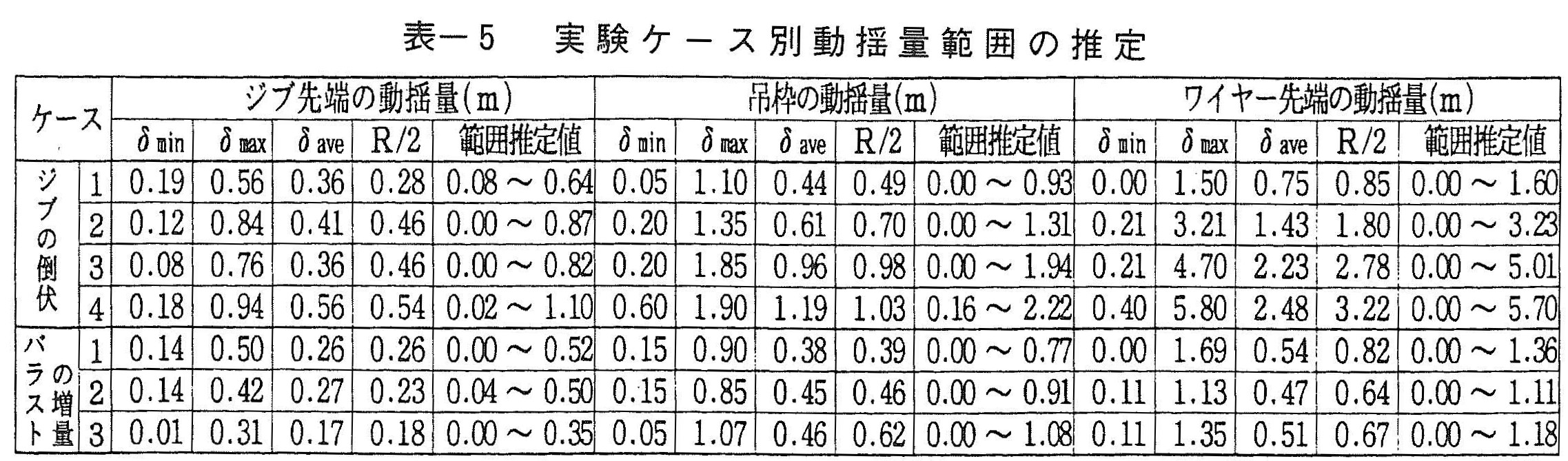
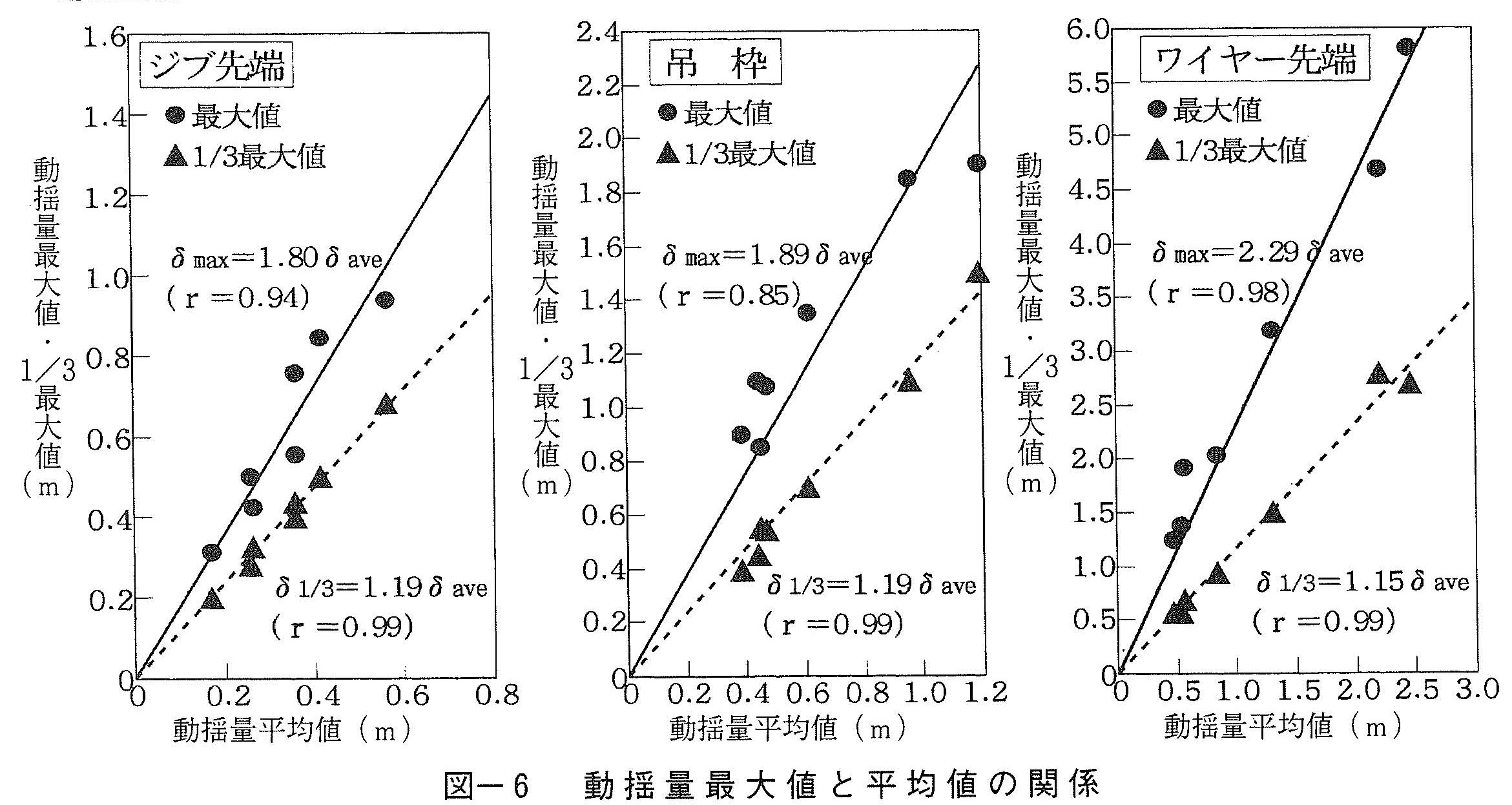
また,動揺量最大値および1/3最大値と平均値の関係(図ー6)は一次式で表せ,最大値は平均値の約2倍程度となった。表ー5を参照すると,R/2の値が動揺量の平均値δaveにほぼ等しく,式(1)より最小値がδmin≒0,最大値がδmax≒R(≒2δave)となることから最大値が平均値の約2倍程度になったものと考えられる。
一方,1/3最大値は,平均値の約1.1~1.2倍であり,一連の動揺量の約66%が平均値程度以下になるものと推察される。
以後で動揺特性を考察する場合には,動揺量の最大値が平均値の約2倍であることを念頭に置いたうえで,動揺量平均値に着目するものとする。
b)各方向別の動揺量
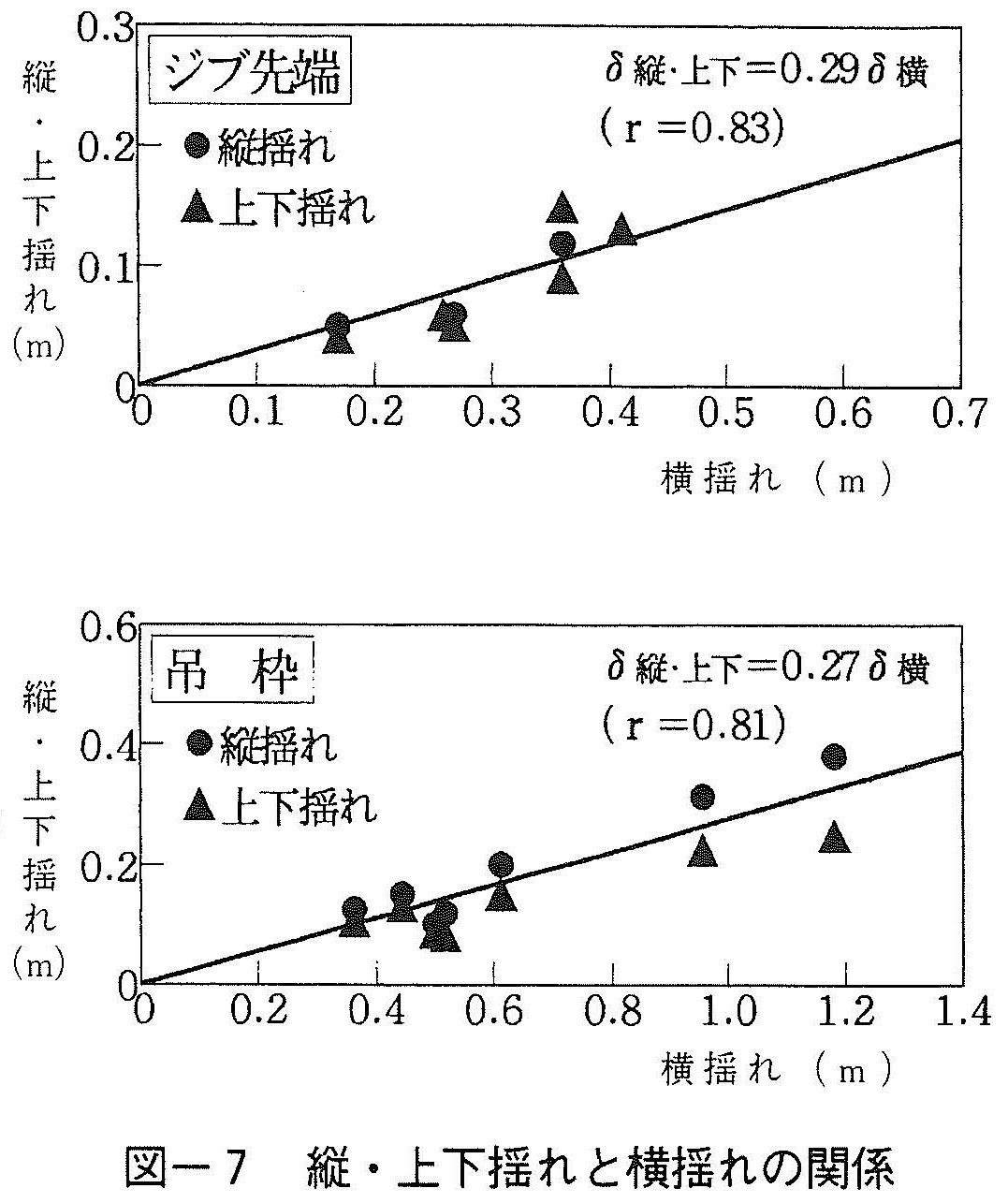
図ー7に,ジブ先端と吊枠のそれぞれについて,横揺れに対する縦揺れおよび上下揺れの関係を示すが,それぞれの対横揺れ比率の値が概ね0.3程度とほぼ等しく,比較的良い相関関係を示す。
これより,動揺量については,揺れの方向に着目すると横揺れが最も大きく,縦揺れおよび上下揺れの大きさは,横揺れの約0.3倍として横揺れの値から推測可能と考えられる。なお,動揺平面軌道については,ジブ先端および吊枠がほぼ相似な楕円軌道を描くことを目視観察から確認している。
測定値からは,平面軌道に関して直交する二方向上でしか確認できないが,目視観察結果も考慮すると動揺平面軌道は楕円軌道で,その形状については,吊枠およびワイヤー先端ともに,長径と短径の比がおよそ0.3のほぼ相似な楕円であると考えられる。
ジブ先端の動揺平面軌道と吊枠の動揺平面軌道がほぼ相似な楕円軌道と考えられることから,吊枠はジブ先端に追随して運動するものと推察される。
以上より,吊枠の動揺については,支点(ジブ先端)に周期的な動揺変位が作用する強制振動状態の振子運動とみなすことが可能と考えられる。
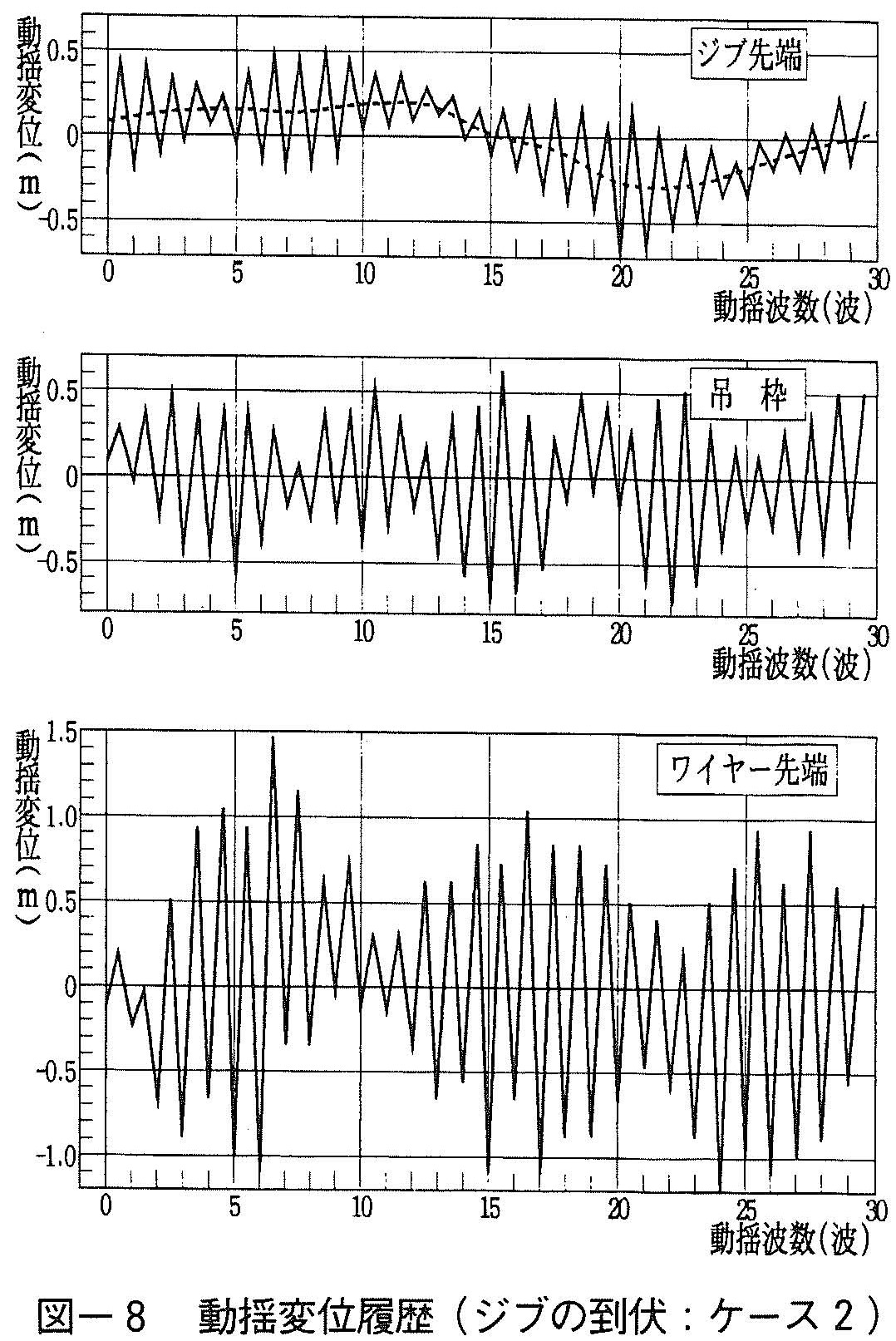
c)動揺変位の履歴
横揺れ動揺履歴の一例を図ー8に示すが,他の実験ケースも同じ傾向を示した。
なお,動揺量の大きさに関する検討を主目的としていることから,計測開始時点からの動揺波数を横軸に採用し,先に述べた動揺周期の値を参考に,必要な場合のみ波数を時間に換算して特性を述べることとする(横軸最小目盛≒7.3秒)。
①ジブ先端の動揺変位は増減変動を繰り返すが,吊枠およびワイヤー先端の動揺変位も増減変動を繰り返す。計測開始時刻がそれぞれ異なるため,図では確認できないが,ビデオAから,ジブ先端,吊枠およびワイヤー先端の動揺量増減変動はほぼ対応していることを確認した。
②ジブ先端の動揺変位には,約2分以上の長い周期成分(図ー8中の破線参照)が含まれている。起重機船の係留ワイヤーの角度は,先に掲載した図ー5に示すように船首側と船尾側で異なっており,ほぼ静止していた船首側に対し,船尾側での移動量が相対的に大きいことは目視で確認できた。このため,②のような動揺履歴が生じたと考えられるが,移動の周期が船対動揺周期の20倍(2分30秒)以上と長く,船対移動が吊枠等の動揺量に及ぼす影響はないと考えてよい。
なお,実作業において問題となるのは,約7~8秒の短周期成分の動揺振幅が大きい場合であり,以後の検討では船対移動を無視するものとする。
4 理論的考察
(1)吊枠の動揺量計算式の誘導
動揺の理論的考察を行う場合,3次元空間における立体的なモデルを取り扱うべきであるが,計算が煩雑なことから,ここでは,2次元の平面的な解析で近似するものとする。
また,先に考察したとおり問題となるのは横揺れによる動揺量であると考えられることから,横揺れに着目するとともに,動揺量計算式の誘導では,支点に周期的な変位が作用する強制振動状態の振子として検討を行うものとする。
ここでは,周期的な変位を正弦波状変位と仮定する。
正弦波状変位が支点に作用する強制振動状態の振子の運動方程式は次式で表される3)(図ー9)。
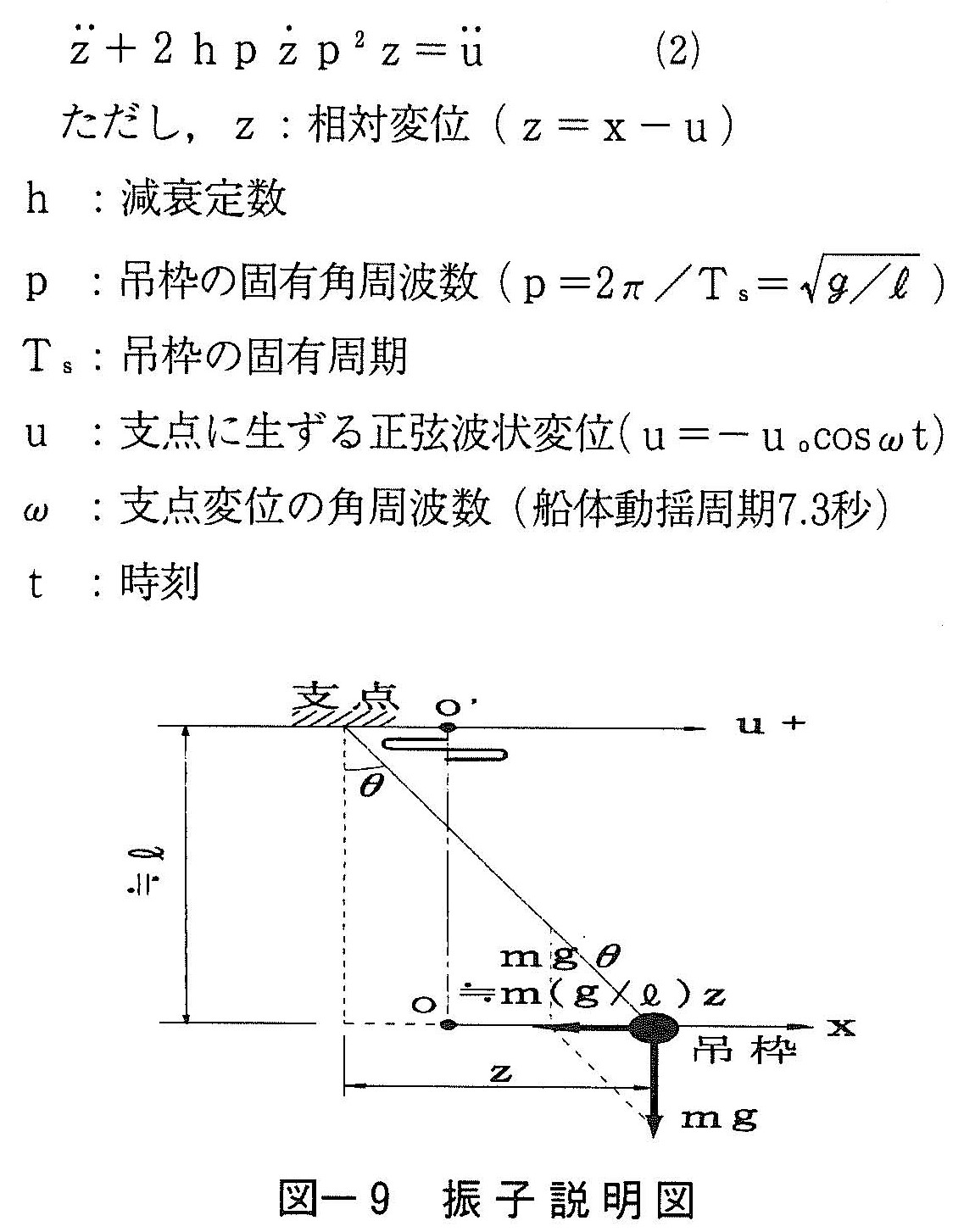
式(2)の解より動揺変位xは次式で表せる4)。

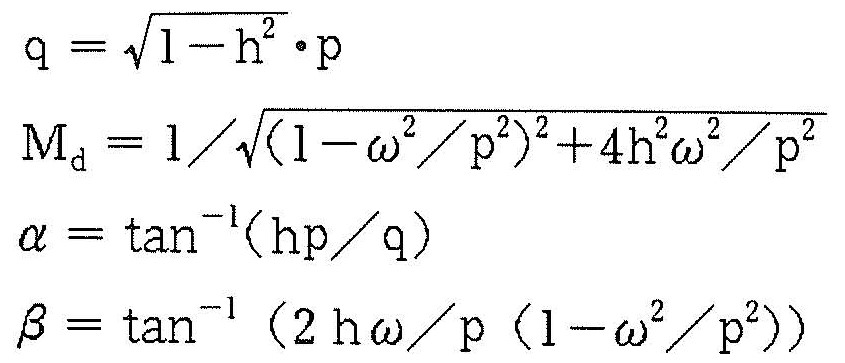
上式(3)より,吊枠の動揺変位は支点の動揺変位(第1項),吊枠自身の動揺変位(第2項)および支点移動に伴い吊枠に伝達される動揺変位(第3項)の和で与えられる。このうち,第2項は時間の経過に伴い0に収束し,位相角βは近似的にπとみなせることから,吊枠の動揺計算式は次式(4)のとおりとなる。

(2)吊枠の動揺増幅率Mdの算定
吊枠の動揺量計算式(5)における増幅率Mdを算定するために,減衰定数hを設定する必要がある。
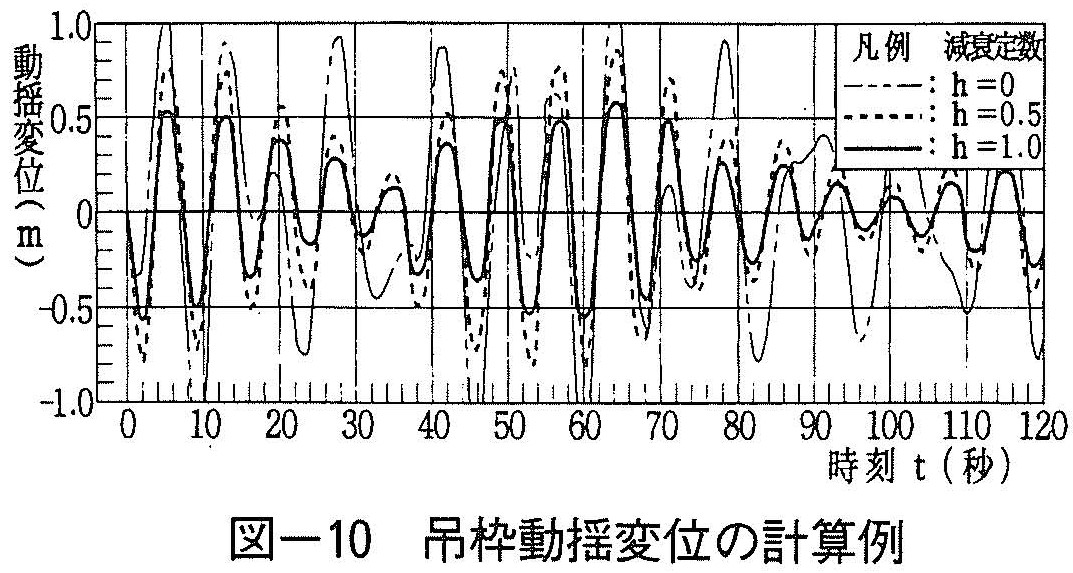
図ー10に,ジブ先端の動揺変位の測定値を入力値として与えた場合の,吊枠の動揺変位を減衰定数別に計算した結果の一例(ジブの倒伏:ケース2)を示す。
減衰を無視(減衰定数0)した場合,吊枠の動揺周期は船体動揺周期と異なるが,減衰を考慮した場合,船体動揺周期7.3秒に近づき,動揺量の増減変動も図ー8に示した実測結果の考察と同じくジブ先端に対応したものとなる。なお,この特性は,計算例に示した実験ケース(図ー10)以外についても同様であった。
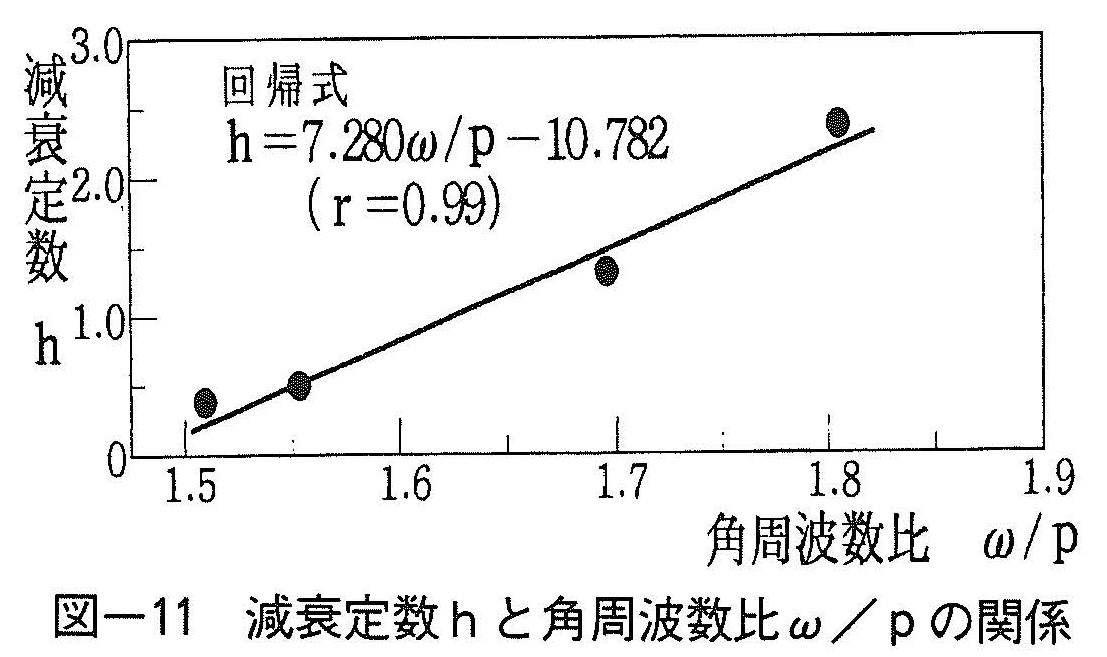
ここで,吊枠動揺量の計算値が測定値と一致するよう仮定した減衰定数hとω/pの関係を図ー11に示す。相関係数はr=0.99となり,かなり良い相関関係がみられるので,この範囲内でのhの推定には,式(6)を用いることとする。
h=7.280ω/p=10.782··········(6)
なお,上記方法により設定される減衰定数hが大きめの値になっており,今後確認を必要とする課題と考えられるが,これについては,特に,40本のケーソン用吊ワイヤーと吊枠との接触部(ガイド部)における摩擦抵抗によるものと考えられる。
すなわち,動揺量が大きい時には,吊枠から白煙を発生(夜間には火花が散乱)し,ガイド部に断面欠損を生ずるほどの痕跡が残っていることから,摩擦抵抗がかなり大きく,減衰も大きくなったものと推察される。また,ワイヤー重量が大きく,これを無視した計算式の適用にやや無理があることも,上記の一因と考えられるが,実工事における動揺量について計測結果と計算結果がよく一致(後述)していることから,現時点では,本報告で設定した減衰定数の値を用いることとする。
(3)ジブ先端動揺振幅uoの算定
ジブ先端では,船体が波の影響により傾斜した分の動揺が生じ,振子の支点に正弦波状変位として作用する。海水面波形と船体傾斜角との関係から,船体は排水量の影響を受けて傾斜すると考えられる(図ー12)。
半周期ごとの平均水位は,波の山でH/π,波の谷でーH/πとなり,船体の傾斜角は次式で求められる。
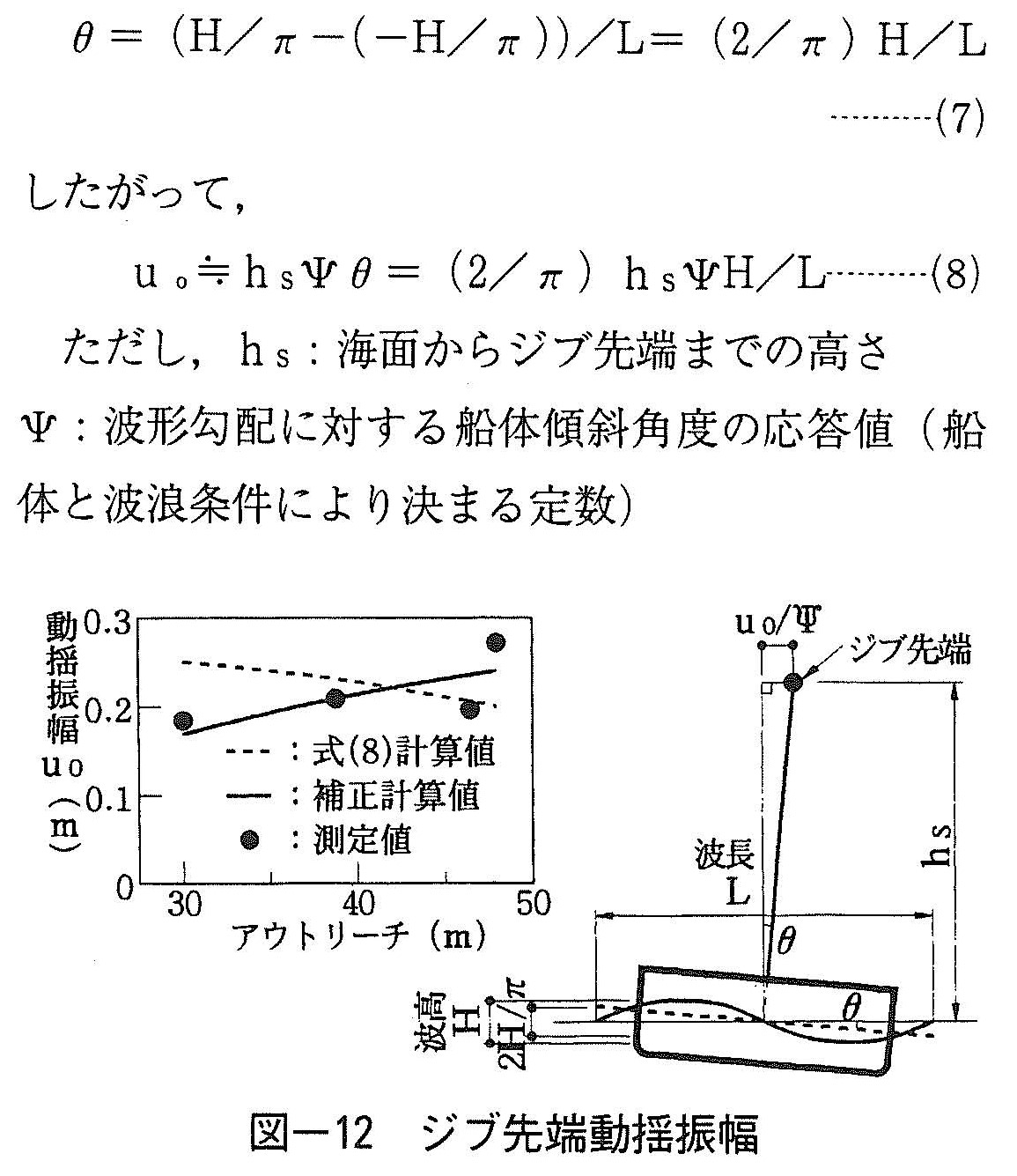
ジブ先端の動揺量uoについて,図ー12に,式(8)で求められる計算値(図中点線)および測定値(●印)を示す。
図より,式(8)によるジブ先端動揺量の計算値は,測定値とほぼ同じ値となるものの,アウトリーチの増加に対する測定値の増加傾向とは逆に,減少傾向となっている。
この原因として,ジブ倒状によりアウトリーチが増加すると,ジブ先端では,船体のヨーイングの影響を受け易くなること等が推察されるが,今回の実験ではヨーイングの計測を行っていないため,原因を解明するまでに至っていない。
ここでは,アウトリーチに対するuoの増加傾向も考慮することとし,式(8)で求めた計算値をuo,測定値をuomとして,両者の比ξ=uom/uoについてジブ高さhsに対する回帰分析を行った。その結果,式(9)の相関関係が得られたので,これを補正係数と考え,式(8)から求められる計算値uoにξを乗じることとした(図ー12参照)。
ξ=uom/uo =-0.032hs+3.022··········(9)
(4)ワイヤー先端動揺量の計算値と計測値との比較
a)ジブの倒状対策
ワイヤー先端の動揺量は,吊枠動揺量の値から初期変位が与えられ,自由振子として計算できる。
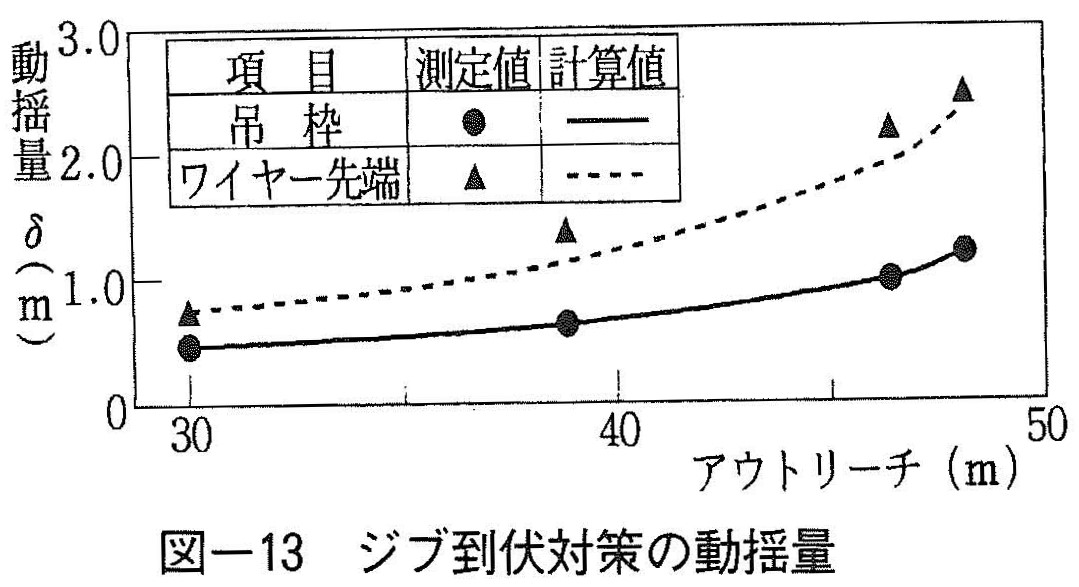
図ー13に,ジブの倒状に対する吊枠,ワイヤー先端の動揺量測定値と計算値の結果を示すが,ジブを倒す(アウトリーチを伸ばす)に従い,吊枠およびワイヤー先端の動揺量が増加する傾向を示した。
これは,ジブを倒すと振子長が短くなるので,吊枠の固有周期(角周波数比ω/p)が小さくなり,強制側ジブ先端周期に近づく,すなわち,吊枠の動揺周期がより同調傾向になるためであると考えられる。
以上より,ジブの倒状対策は,吊枠および吊ワイヤー先端の動揺量が増加することから,むしろ逆効果となることがわかった。
b)海水バラストの増量対策
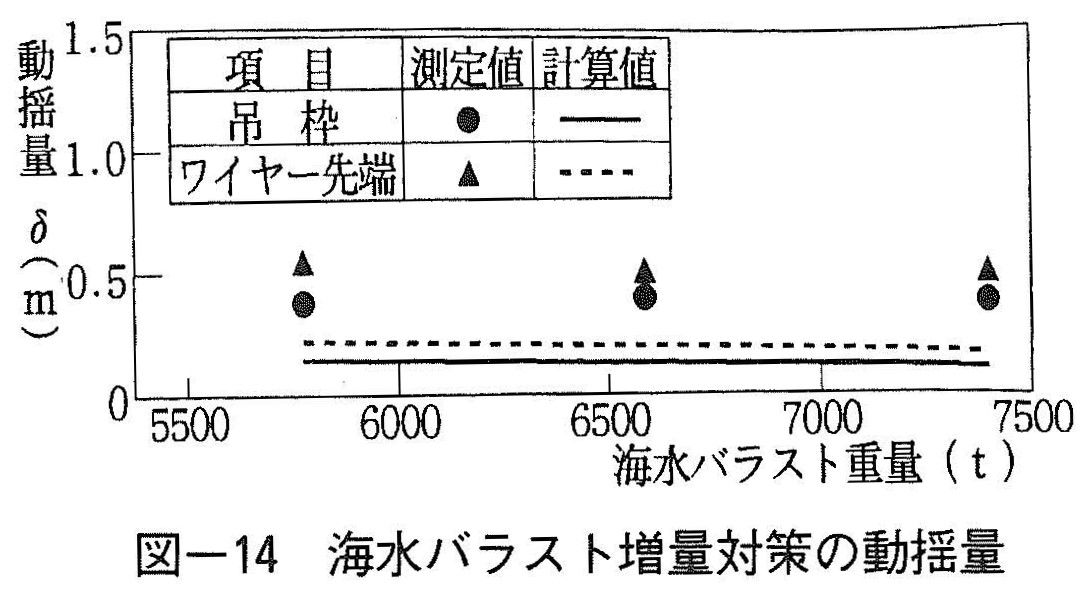
図ー14に,海水バラスト増量に対する吊枠およびワイヤー先端の動揺量と海水バラスト重量との関係を,また,表ー6に,ワイヤー先端の測定値と計算値を示すが,動揺量低減効果はそれぞれ3cmおよび6cm程度となった。
測定用目盛板の最小目盛間隔は20cmで,約280m離れた位置からトランシットで読み取っており,測定値には約5~10cm程度の誤差を含むものと考えられる。
よって,海水バラスト増量実験では,波浪条件が静穏なため動揺量絶対値に対して測定誤差が大きく,ワイヤー先端の動揺量測定値から低減効果を確認できなかったと考えるのが妥当である。

c)動揺低減効果の推定
実験結果に基づく式(5)~(8)を用いて,無対策とバラスト増量時におけるワイヤー先端動揺量と波の周期との関係を整理し図ー15に示す。図中の破線は,従来の作業可能範囲の動揺量(0.4m)を示す。なお,●印は実工事における動揺量測定値,〇印は計算値であり,これについては5で後述する。
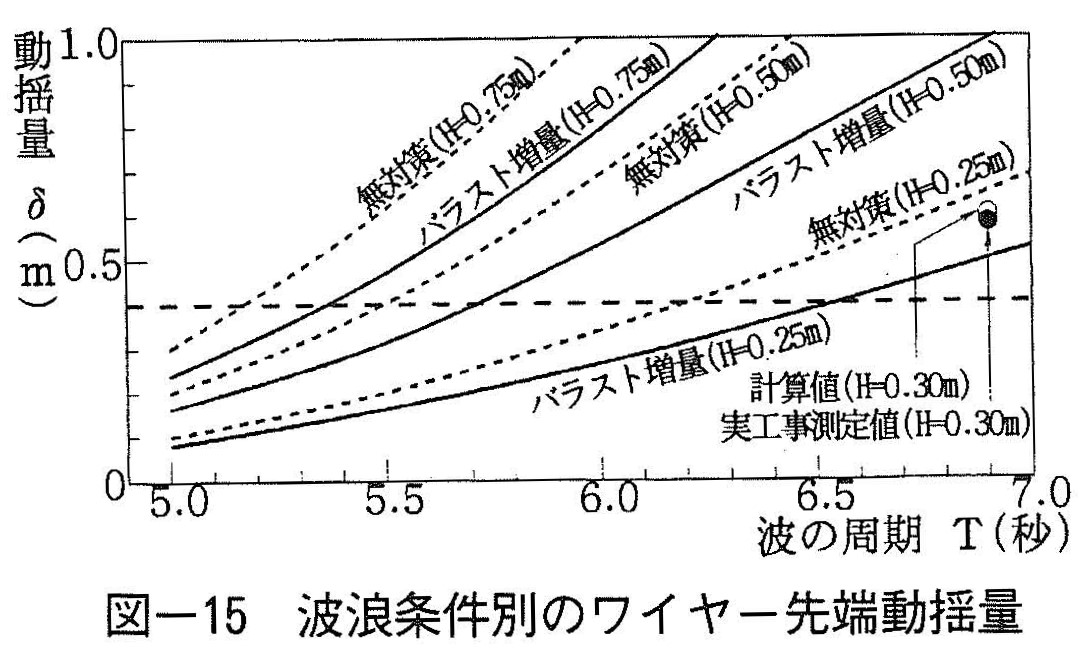
図より,波高と周期が同じ条件では,バラストを増量した場合の動揺量が,無対策時(通常のバラスト量)の動揺量に対して,およそ2割程度小さいことがわかる。
また,波高が0.5mの場合,バラスト増量により約5.7秒まで無対策時の動揺量以下となり,動揺低減効果を波の周期に換算すると,0.2秒程度a)長くすることが可能と推測される。
波高が0.5m以外の場合でも,作業条件の改善効果は0.2~0.3秒程度でほぼ一定とみなせる。
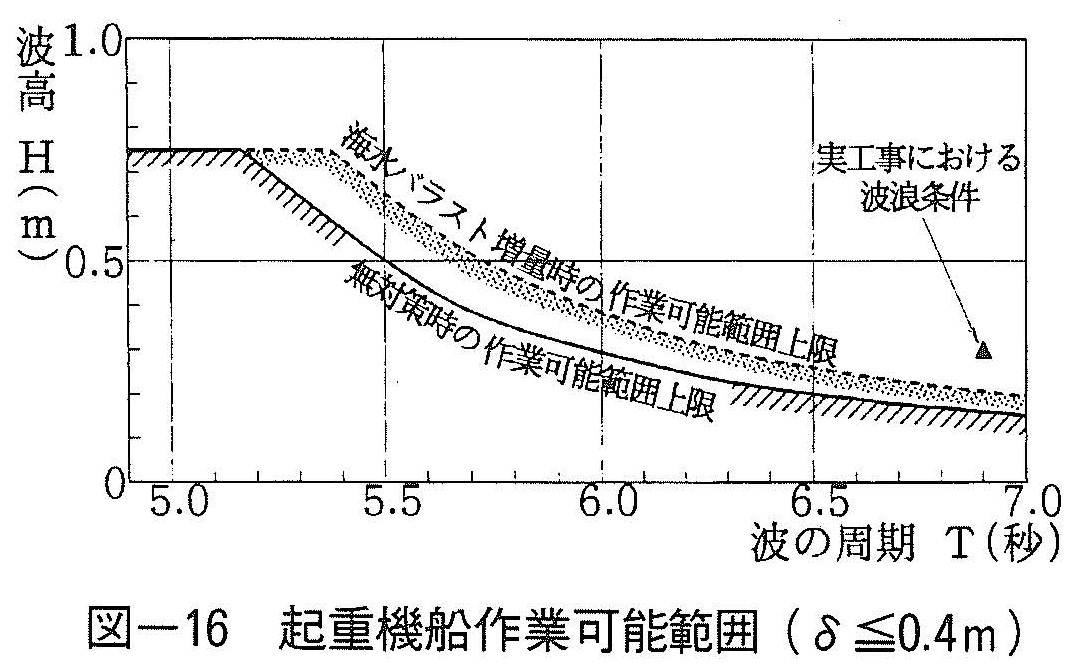
次に,図ー15で5≦0.4mとなる波高と周期の組合せを抽出すれば,開閉作業可能範囲を波浪条件で表すことができる(図ー16)。図は,周期が与えられた場合その周期に対する特性曲線上の波高以下,波高が与えられた場合には特性曲線上の周期以下となる波浪条件を作業可能範囲とするものである。また,▲印は実工事における波浪条件であるが,これについては5で後述する。
波高の上限を0.75mとしたのは,起重機船作業に必要な揚錨船等小型船舶の作業限界を考慮したものである。
5 2番船入船時における対策適用結果
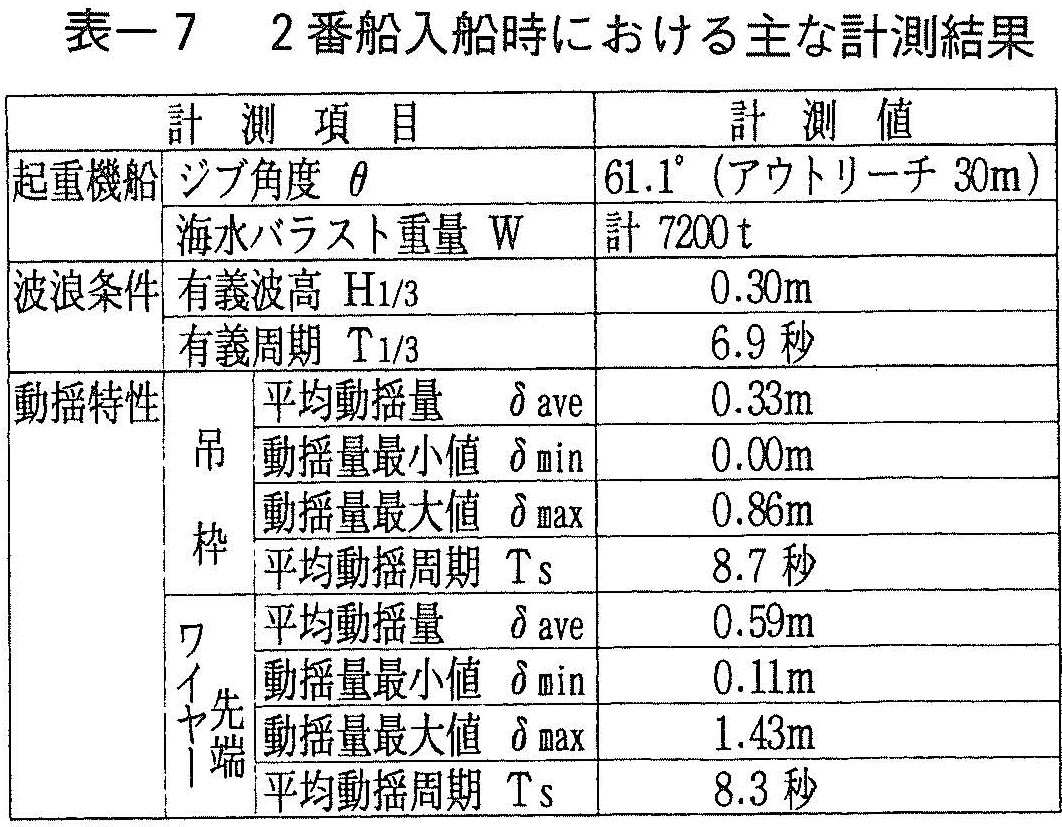
実験後の平成6年6月22日,2番船入船に伴う開閉工事を実施した。波高0.30m,周期6.9秒と波浪条件が悪かったことから海水バラストを追加投入(増量)し,工事と並行して,ケーソン玉掛け前における吊枠および吊ワイヤー先端の動揺量を中心とする計測を行った。主な計測結果をまとめて表ー7に示す。
吊枠およびワイヤー先端の動揺周期は,実験で得られた吊枠の平均動揺周期約8秒に対して,若干大きめの値ではあるものの,ほぼ同じ値となった。
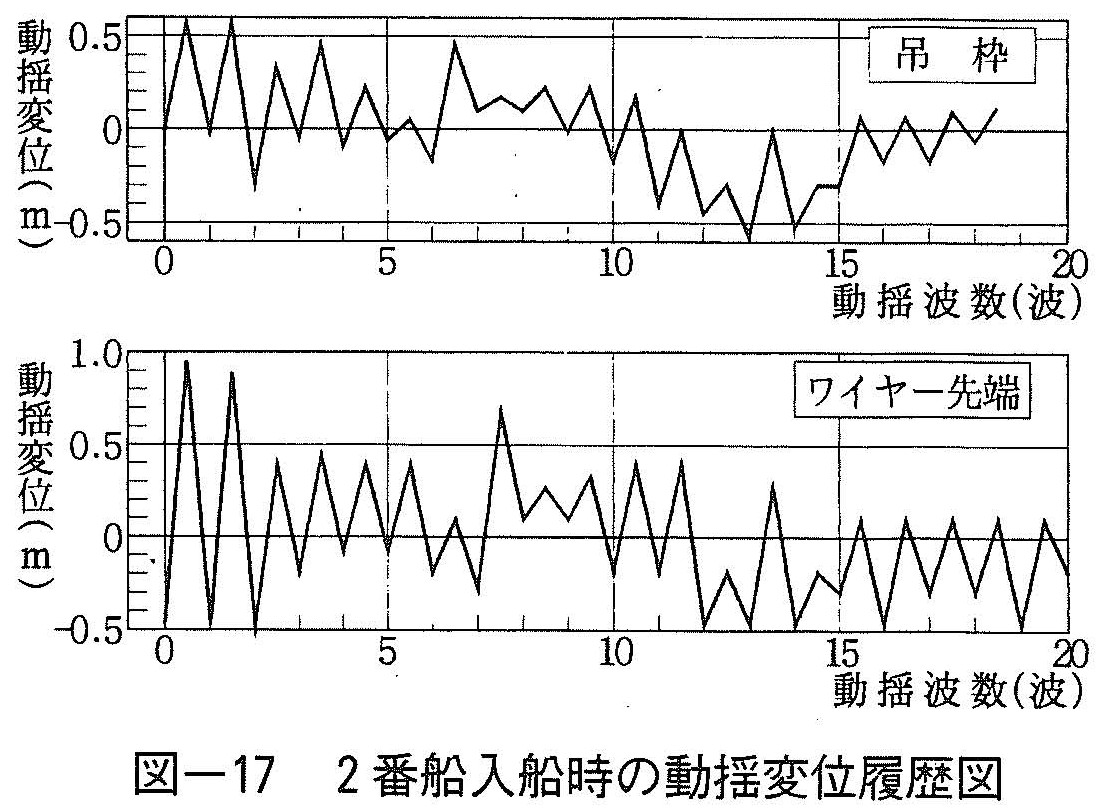
動揺変位履歴は図ー17のとおりであり,吊枠およびワイヤー先端の動揺変位が増減変動を繰り返す等の特徴は,実験から得られた結果(図ー7)にほぼ一致する。
さらに,ワイヤー先端動揺量について,前述の動揺特性曲線上(図ー15)に,実工事中の測定値●と,実工事の波浪条件(波高0.30m,周期6.9秒)に対するバラスト増量時の計算値0を図示すると,測定値は,バラスト増量を考慮した計算値とほぼ一致することがわかる。
また,前述の図ー16に,観測された波浪条件▲を示すと,起重機船の作業可能範囲から外側にはずれているが,実作業においても,海水バラストを追加投入しただけでは,ワイヤー先端の動揺量が大きく,そのままでは安全な作業性確保に問題があったので,さらに介錯ロープを用いて4人掛かりで1本ずつのワイヤーを拘束することにより,ワイヤー先端動揺量を0.4m以内に抑えて作業を実施した。
以上より,2番船入船時開閉工事における計測結果は,実験で得られた作業可能範囲に関する図一16の妥当性を裏付ける結果であったものと考えられる。
6 まとめ
実験結果から,次のことが判明した。
1)支点に正弦波状変位が作用する強制振動状態の振子を仮定して計算した動揺量と測定から得られた動揺量とがほぼ一致する。
2)起重機船のジブ倒状対策は,むしろ逆効果である。
3)海水バラスト増量対策については,実験から直接動揺低減効果を確認できなかったものの,2番船入船時の計測結果を用いた検討から,実験結果に基づく推定がほぼ妥当であったものと考えられる。
4)起重機船のジブを最大高さまで起こし,海水バラストを増量することにより,動揺量を2割程度低減でき,その低減効果を波の周期に換算すると,約0.2秒程度の作業限界条件の向上となる。実工事での計測結果も,これを裏付けるものとなった。
7 おわりに
今回の実験に用いた起重機船については,稼働効率をわずかながら向上させることが可能であることを確認した。
ただし,海水バラスト増量対策の動揺低減効果については,工事海域の波浪条件は勿論のこと,使用する起重機船の種類によっても異なるものと考えられる。例えば,船体の固有周期が短ければ,同じ波浪条件下でも船体の動揺量が大きくなるであろうし,追加投入可能なバラストタンクの容量が十分に大きくなければ,稼働効率の向上は望めないことになる。
したがって,使用する起重機船の諸元等を事前に調査するとともに,対策の適用可能性を十分検討しておくことが肝要である。
今後,当工事において,さらに効率的な玉掛け方法の改善を図る等の工夫により,開閉工事全体の作業性を高めてゆくことに努力したいと考える。
参考文献
1)鐵 健司:品質管理のための統計的方法入門,日科技連出版社,1985.
2)堀川清司:海岸工学,東京大学出版会,1973.
3)岡本舜三:建設技術者のための振動学,㈱オーム社,1976.
4)土木学会:構造力学公式集,1986.




