構造物の制振制御装置と機能(その1)
九州大学工学部助教授
烏 野 清
1 はじめに
近年,新しい建設材料の開発や施工技術の発展に加え,コンピュータによる解析法の進歩により,土木・建築構造物が大型化すると共に,振動の発生し易い構造形式が多くなっている。また,環境問題等により景観重視の設計が採用され,従来よりスレンダーな構造物も建設されている。これらの構造物が大地震時,強風時に十分安全であるように耐震,耐風設計の検討されなければならないが,通常の風や車両走行時に発生する振動に対しても,人体に対する不安感や構造材料の疲労問題等から,検討を行う必要が起きている。以上のような状況から,制振,免振装置の開発が最近注目されるようになっている。
本講座は振動問題に対して,苦手としておられる方のために,構造物の振動制御装懺と機能に関する解説を行ったものである。
2 構造物の基本的応答特性
構造物が地震や風の外力を受けた場合の基本的な振動(応答)特性を知るために,図ー1に示すように重量W,ばね定数k,粘性減衰係数Cを持つ簡単な1質点系モデルに正弦波外力Pcos ω tが作用している場合を考えてみる。
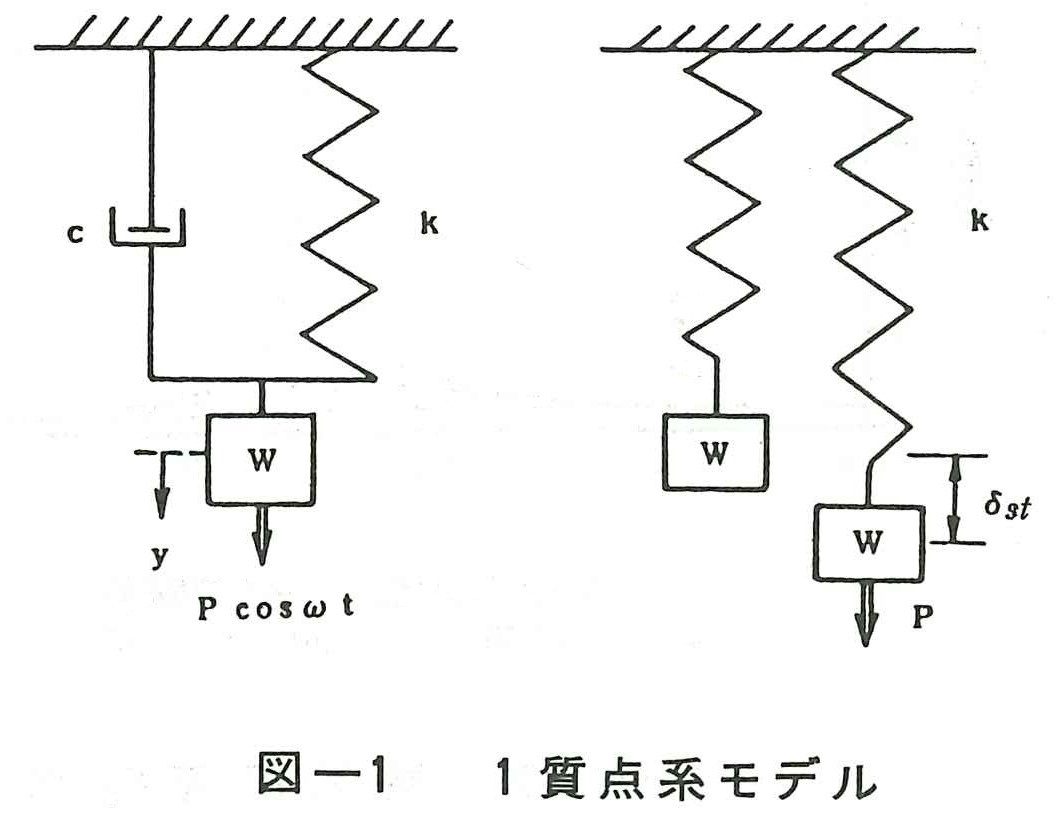
運動方程式は次式となる。

W/gは質量で重量を重力加速度g(=980cm/s2)で除したものである。
(1)式をW/gで割ると次式が得られる。
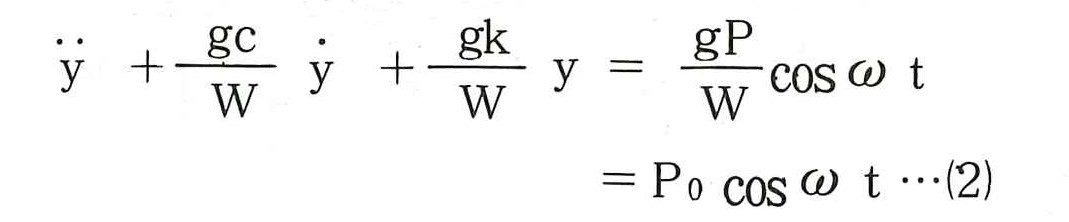
(2)式を通常用いられる振動方程式に書き直すと次式となる。
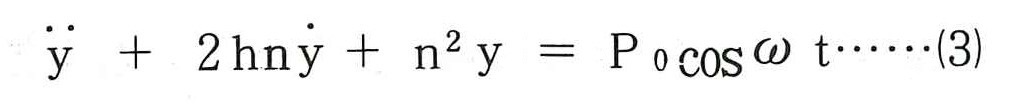
(2)式と(3)式の左辺の係数の関係から,次式が得られる。
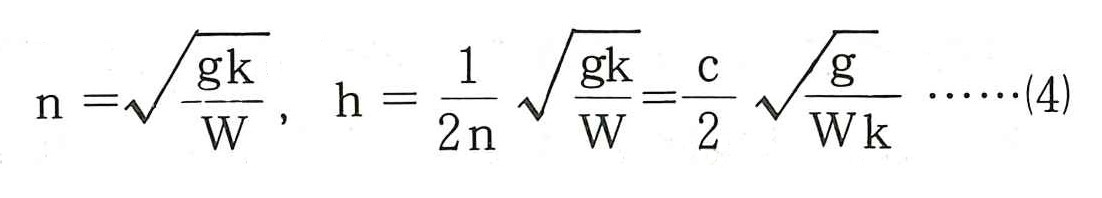
(4)式のnは図ー1に示すモデルにおいて,c=0の場合の固有円振動数(rad/s)で,WとKによって決まる固有の値である。このnと通常用いられる固有周期T(sec),固有振動数f(Hz)の間には次の関係がある。
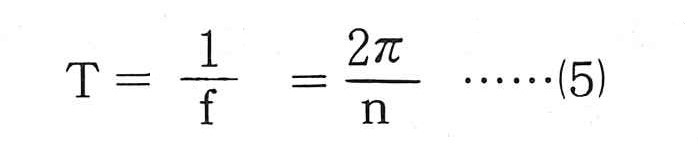
一方,(4)式に示すhは減衰定数と呼ばれるものであるが,実際の構造物では粘性減衰係数cの値が不明なため,振動試験等により直接減衰定数の値を求めることが多い。この減衰定数は構造物の応答に大きく影響する値であるが,一般の構造物ではほぼ0.01~0.05,基礎構造物で0.1~0.2程度と考えておけばよい。
(3)式の解は次式で表される。
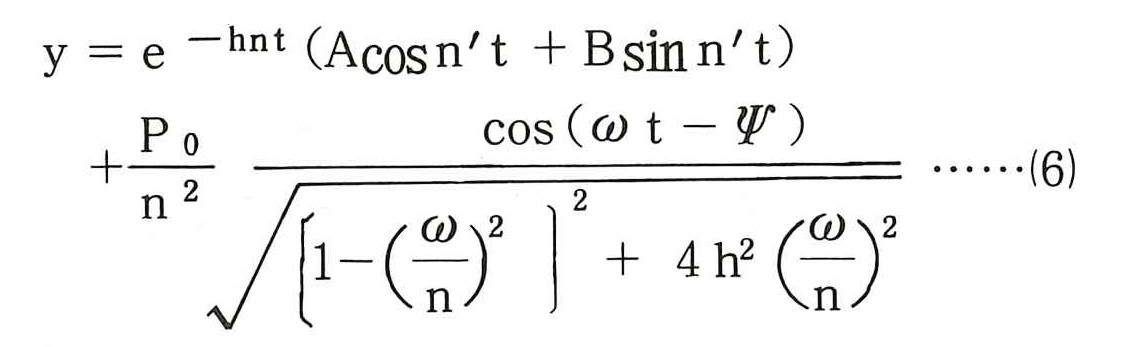
(6)式の第1項は自由振動の項でA,Bは初期条件より決定できるが,振動が始まって十分時間が経過すればこの項は消滅し,第2項の強制振動項のみの応答となる。したがって,振動開始直後の過渡振動の状態を調べなければならない場合には(6)式の第1項と第2項で,強制振動による定常振動を知りたい場合には第2項のみで計算すればよい。
(6)式中のn’はc≠0の場合のモデル系の固有振動数で,(4)式に示すnとは次の関係がある。
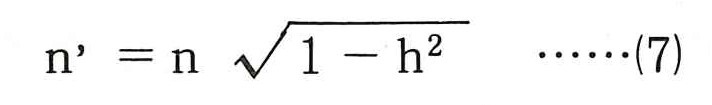
先に述べたように,通常,構造物の減衰定数の範囲である0.01~0.2では,n’≒nとみなしても差し支えない。
(6)式のP0/n2は次のように変換される。
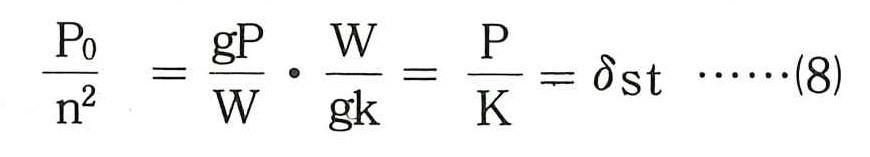
(8)式はモデルにPなる外力が静的(ω=0)に作用した場合の変位δst(図ー1の右側参照)を示しており,(6)式の第2項において,次式はこの変位の応答倍率を示すことになる。
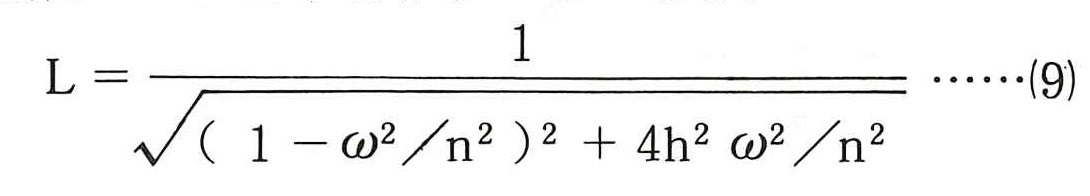
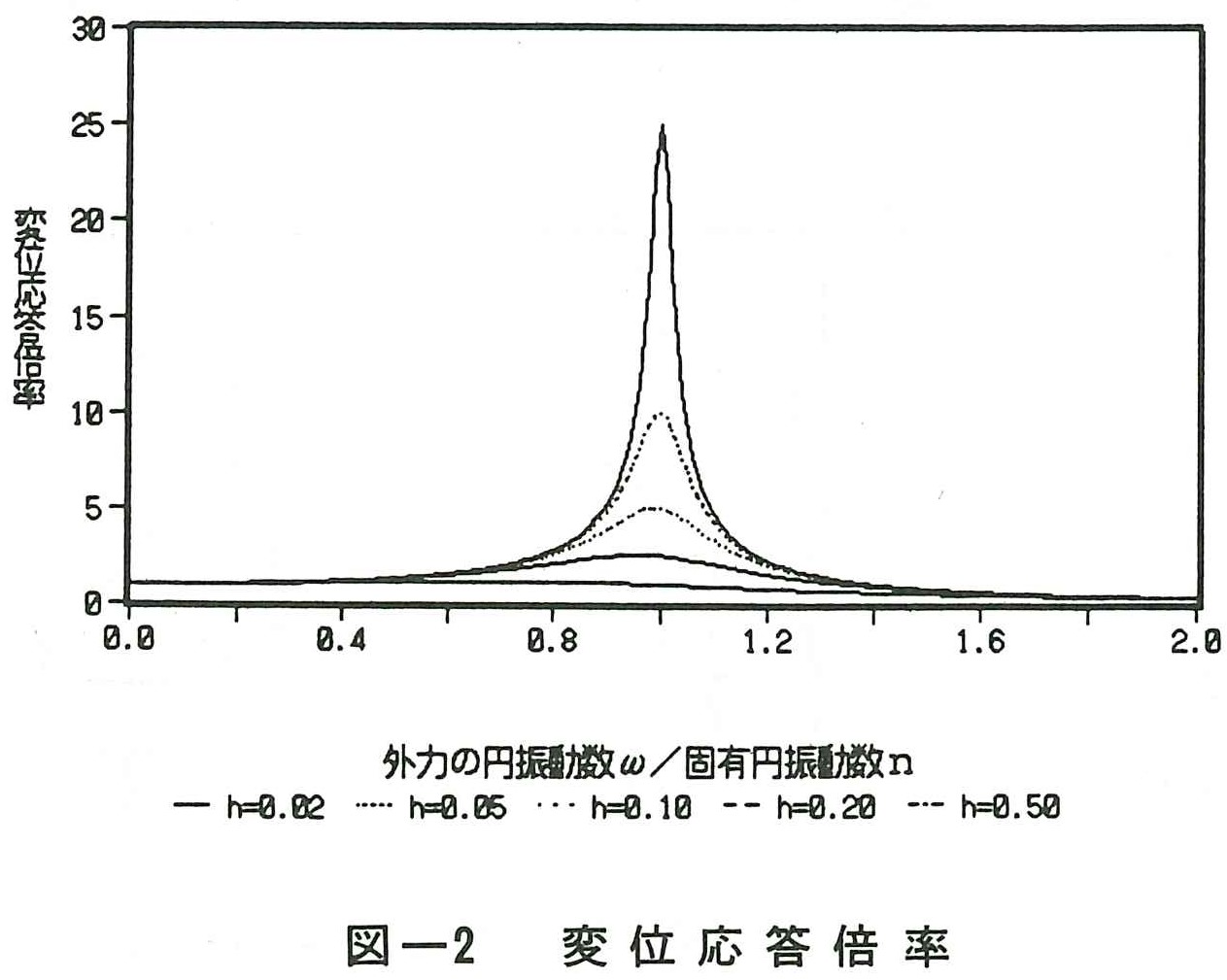
図ー2は(9)式において,外力の円振動数ωを0から徐々に大きくした場合の倍率Lをパラメータω/nで示したものである。図よりω/n =1の場合に変位の応答倍率が最も大きいことがわかる 。つまり,モデル系の固有円振動数nと外力の円振動数ωが一致する時に共振の状態になることを示している。また,減衰定数が小さい程,応答倍率が大きく,(9)式においてw/n=1を代入するとL0の値は次式となる。

(10)式は共振点における応答変位の倍率を示したもので,この式を用いれば簡単に倍率を計算することができるので,覚えておくと便利である。
またω/n >1.4の範囲では応答倍率が逆に1より小さくなり,免振・防振を考える上で重要な特徴を示している。
応答変位を小さくするためには,図一2に示す結果より次のことがいえる。
(1) 構造物の固有円振動数nと外力の円振動数ωを一致させないことが重要である。
この場合,外力の円振動数ωが判っている時には,構造物の円振動数nをなるべく小さくすれば,応答倍率が1以下となり,免振されることになる。nを小さくする方法として,(4)式に示すように重量Wを大きくするか,ばね定数kを小さくしなければならないが,kを小さくすると振動変位が大きくなるため(δstが大きくなる),一般的には重量Wを大きくするのが望ましい。
この特性を利用した制振例としては,振動する機械の基礎構造物の防振として,基礎下端にばねおよびダンパーを設置しているものがある。
(2) 減衰定数を大きくする。
(10)式に示すように,減衰定数は応答倍率に直接影響する事から,構造物の減衰が大きくなる装置を付加すればよい。福岡の斜張橋荒津大橋において風速10mで雨の日にケーブルが大きく振動する,いわゆるレインバイブレーションが発生したため,この対策として,オイルダンパーが各ケーブルに設置された。これはオイルダンパーを用い,減衰を付加することにより制振効果を高めたもので,現在,振動は完全におさまっている。
3 制振装置
3.1 概 要
2で簡単な1質点系モデルの応答特性について示したが,現実の構造物は複雑な構造をした多質点系であり,また外力も正弦波ではなく不規則波の場合もあり,簡単に制振出来ない事が多い。したがって,構造形式等に対応して,数多くの制振装置が考案されている。
構造物の制振方法としては大きく次の3種類に分類される。
(1) パッシブコントロール
① 構造物の質量や剛性を変化させる方法
② 構造物にダンパーまたは動吸振器等の装置によって減衰を付加する方法
③ 構造物の形状を変える事により,外力として作用する空気力を低減させる方法
(2) アクティブコントロール
構造物の振動を小さくする制御力を与えて制振させようとする方法で,高精度センサー類の開発,コンピュータによる制御技術,駆動装置の開発に伴って,機械,造船,航空工学分野で現在幅広く用いられているが,土木,建築分野では構造物が大型であり,大きな駆動力を必要とする事等から実用化されている例は少ない。
(3) ハイブリットコントロール
振動制御力として上記の(1),(2)を併用して用いる方法で,小さい駆動力でより良い制振効果を得ようとするものであるが.現在研究の段階といえる。
制振装置として数多くの種類がある事から,実用化されているものについて,解説を加えていきたい。
3.2 パッシブコントロール
3.2.1 動吸振器
構造物本体に付加系を取り付けた場合のモデルは図ー3のようになる。構造物の固有円振動数n1,減衰定数h1および付加系の固有円振動数n2,減衰定数h2は(4)式を参考にして次式となる。
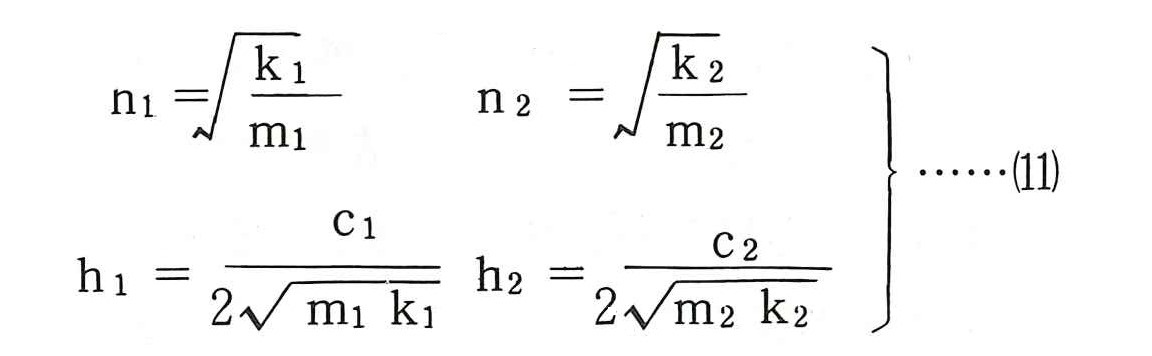
同様に外力に対する構造物系および付加系の静的変位は(8)式より次式で得られる。
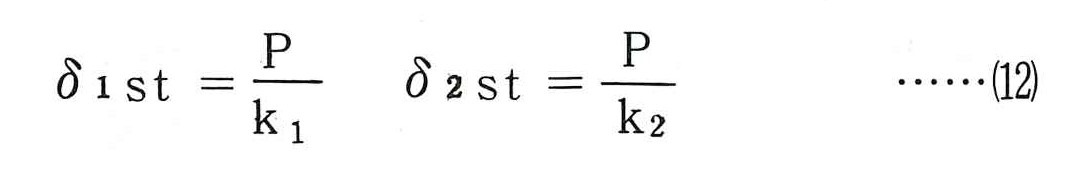
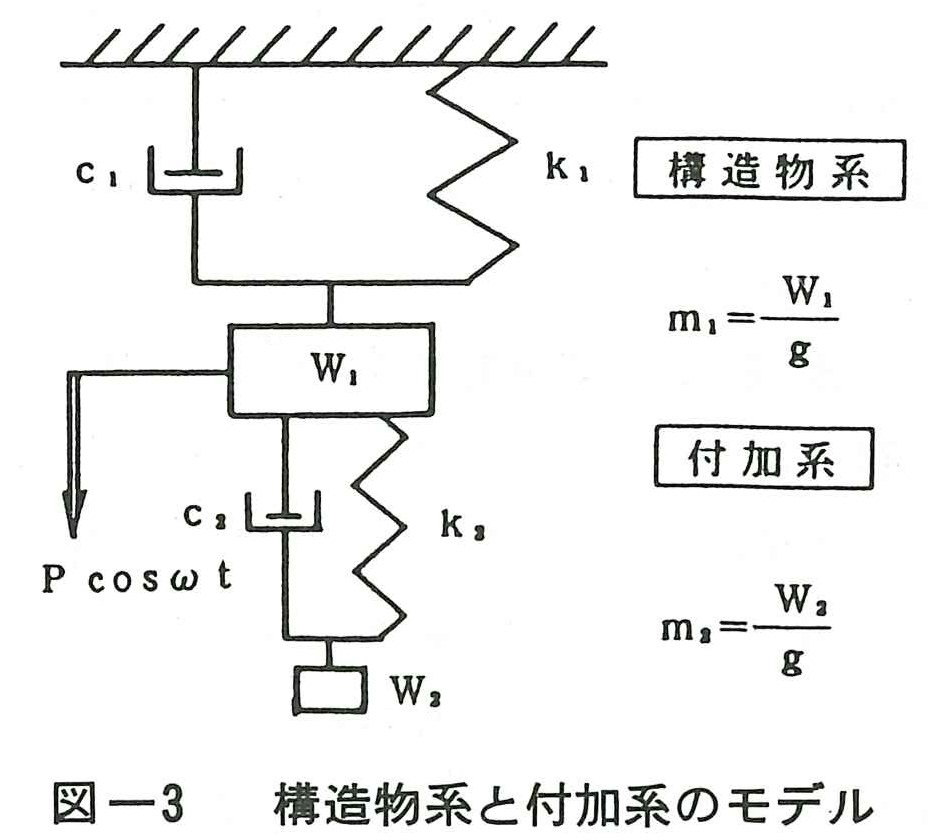
いま,構造物系に対する付加系の質量比をμ,固有円振動数比をα,外力の円振動数に対する構造物系の固有振動数比をβとすると次式となる。
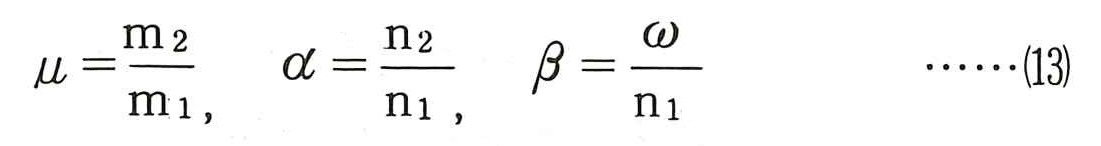
この場合の構造物系および付加系の応答倍率L1,L2は次式で示される。
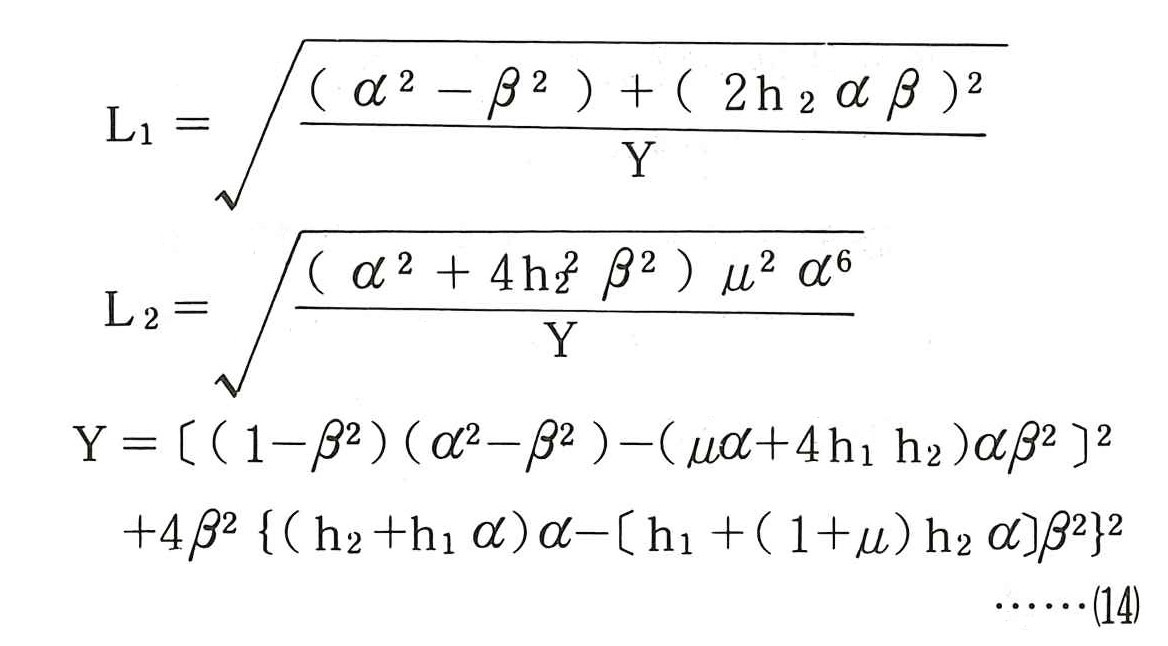
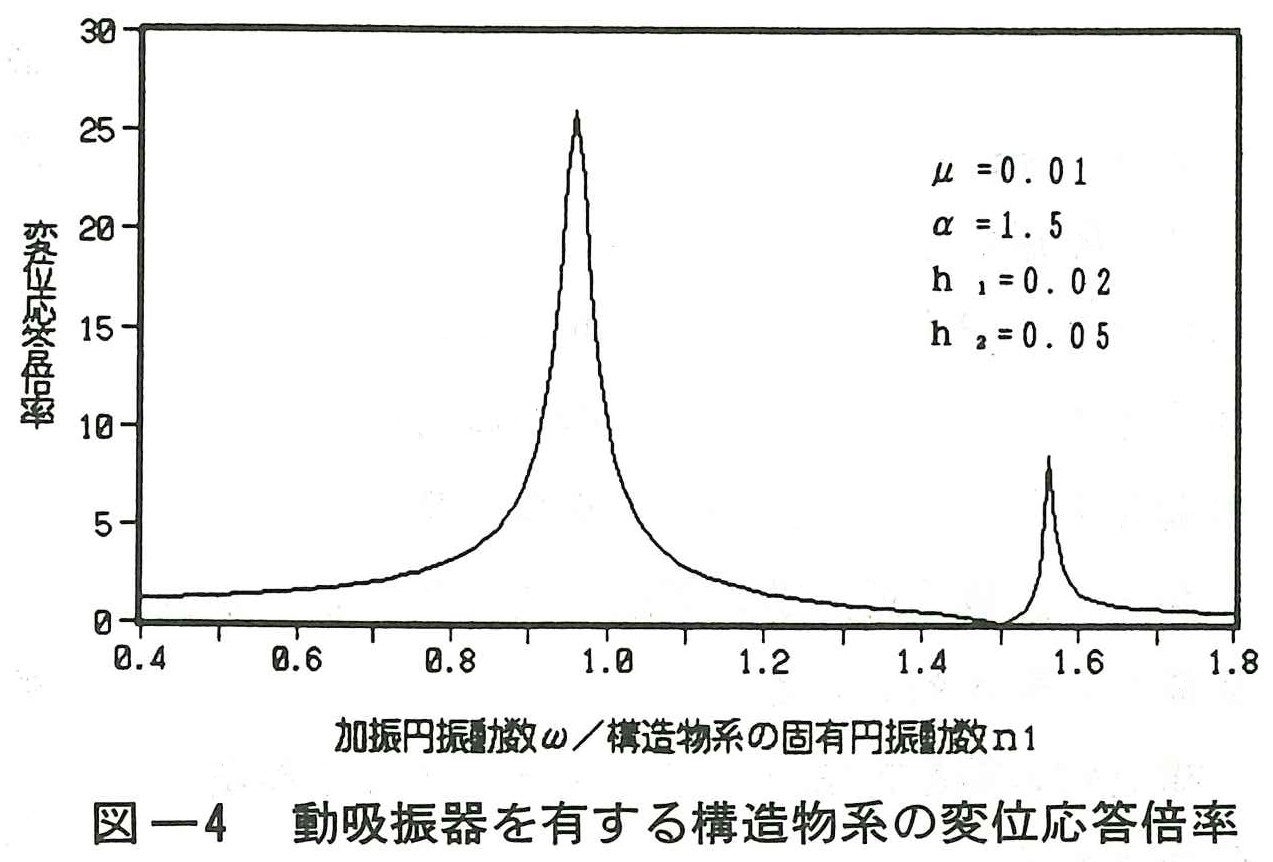
図ー4はμ=0.01,α=1.5,h1=0.02,h2=0.05として,構造物系の静的変位δ1stに対する応答倍率をβをパラメータとして計算したものである。図を見ると,ω/n1=1.5のところで,構造物系の応答変位はゼロとなり,付加系のみが振動する状態となっている。このことは,外力の円振動数ω0が判っている時,構造物系の固有円振動数n1を先の図ー2に示した理由により,ω0より小さく設計し,次に付加系の固有円振動数n2がω0に等しくなるように,質量m2とばね定数k2を決定すれば,構造物系は全く振動せず,付加系のみが振動して,外力の振動エネルギーを吸収することになる。この現象は振動論でいう逆共振の状態であり,この付加系が動吸振器(Dynamic Absorber)と呼ばれる制振装置である。
3.2.2 同調質量ダンパー(TMD)
図ー3に示すモデルにおいて,動吸振器とは異なって,付加系の固有円振動数n2を構造系の固有円振動数n1とほぼ一致させることにより,付加系を共振させ,構造物系の応答変位を制振する装置を同調質量ダンパー(Tuned Mass Damper)といい,通常,略してTMDと称している。
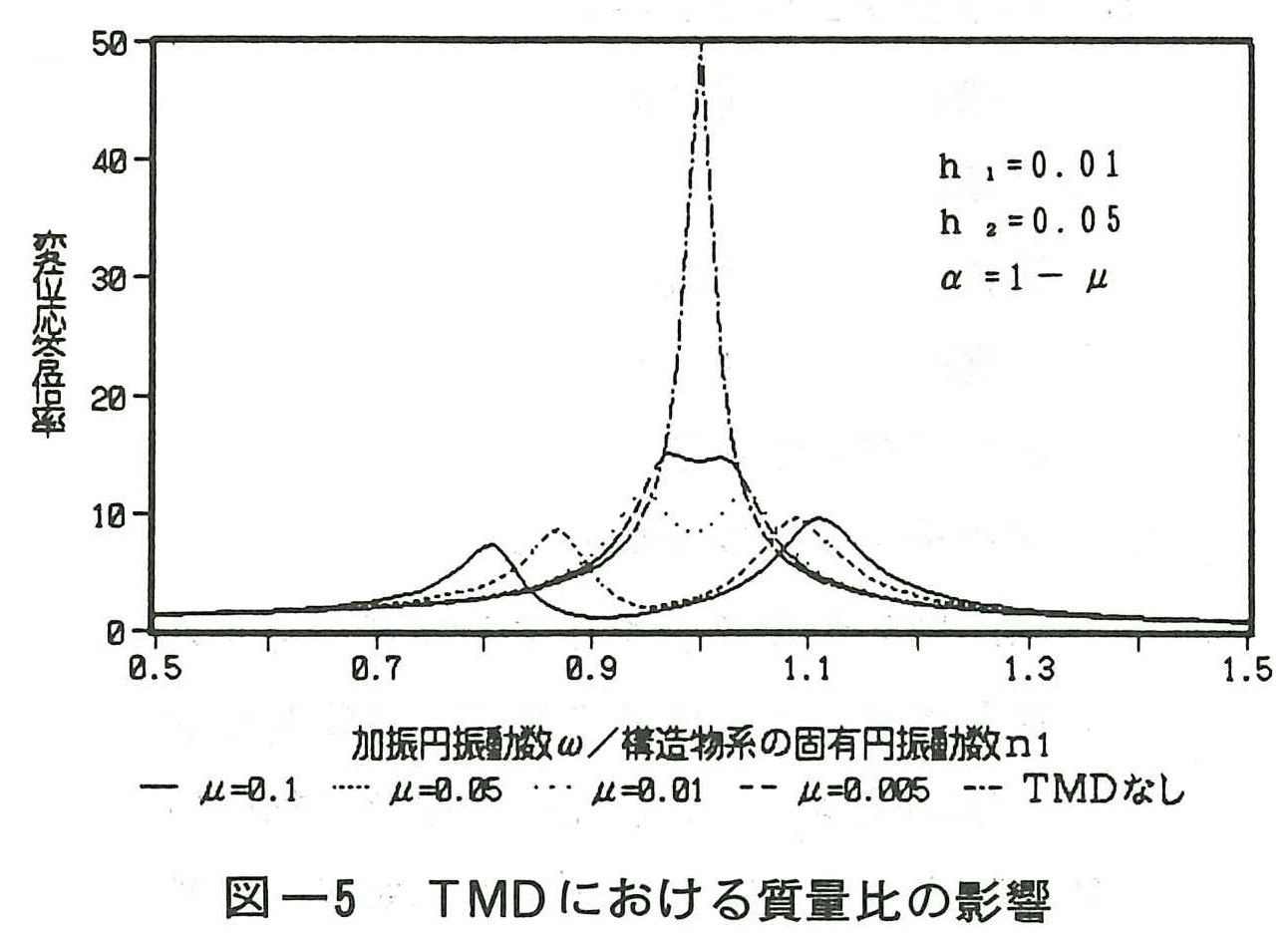
この場合の応答倍率は先の3.2.1に示した動吸振器の場合において,n2/n1≒1としてパラメー夕計算すればよいことになる。図ー5は構造物系に対するTMDの質量比μをパラメータとし,h1=0.01,h2=0.05,α=n2/n1=1ーμとした時の構造物系の変位の応答倍率を示したものである。μが大きくなる程,応答倍率が小さくなり制振効果が大きくなることを示しているが,μ=0.01,つまり,付加質量が構造物系の1%程度であれば,かなりの制振効果が期待でき,それ以上TMDの質量を増やしても,制振効果の割合はそれ程良くならない。また,μ=0.01以上になるとα=1の左右両方にピークが現れる傾向がある。この両ピークはαの値に非常に敏感であり,αが少し変化すると片方のピークが大きくなり,制振効果が悪くなる。つまり,制振するために最適なαが存在することになる。したがって,構造物系の固有円振動数に対してTMDの固有円振動数を設定することがかなり難しく,実際の構造物に設置する場合には,TMDの固有円振動数を微調整する装置が必要となる。
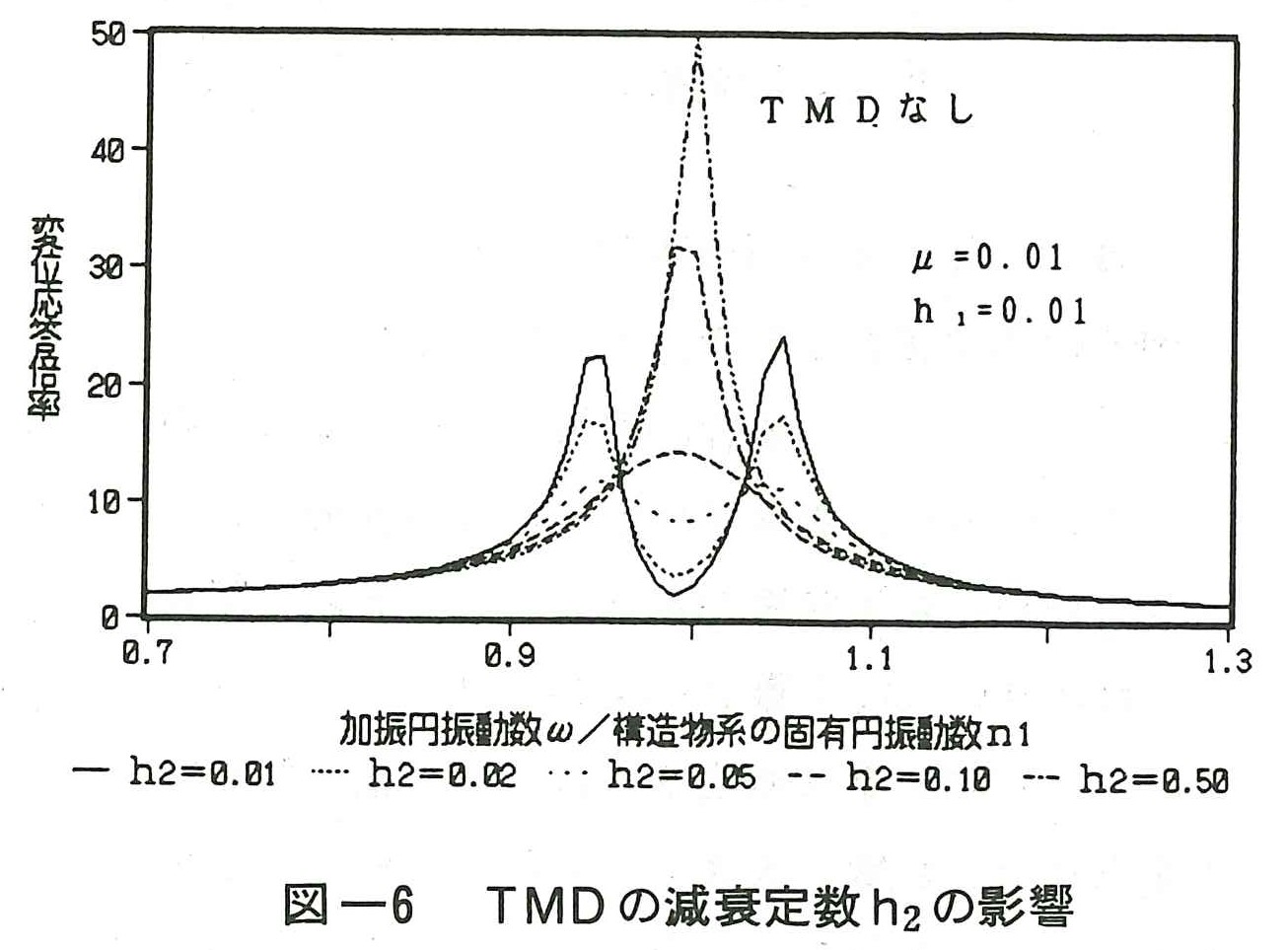
図ー6はTMDの減衰定数h2の影響を調べるために,μ=0.01,h1=0.01としてh2を変化させた時の構造物系の変位応答倍率を示したものである。図ー6によればh2が0.05以下になると2つのピークが明瞭に現れ,かえって制振効果が悪くなっている。一方,h2が0.1より大きくなると構造物系とTMDが一体化して振動するためピークは1個となるが,応答倍率は大きくなっている。この計算例ではTMDの最適減衰定数h2は0.05程度と予想される。
以上示したように,TMDを設計する場合には構造物系の固有円振動数n1や減衰定数h1に対して,TMDとして最適なn2,h2が存在することになる。したがって,(14)式に示す応答倍率の式においてTMDの固有円振動数n2,減衰定数h2,および質量比μ,固有円振動数比αをパラメータを変化させて数値解析すればよい。この解析は簡単にパソコンを用いて計算できるので利用して頂きたい。
このTMDは斜張橋の主塔内部に設置され,風による振動の制振装置としてかなり用いられている。荒津大橋の主塔内部にもこの装置が設置されている。
3.2.3 同調液体ダンパー(TLD,TLCD)
3.2.2に示したTDMは振動質量として剛体を用いているが,容器内の液体の動揺振動(スロッシング)を利用した制振装置が近年,建築の分野で用いられている。この種のダンパーは水を質量とし,重力を復元力とするもので,原理的にはTMDと同じと考えてよい。
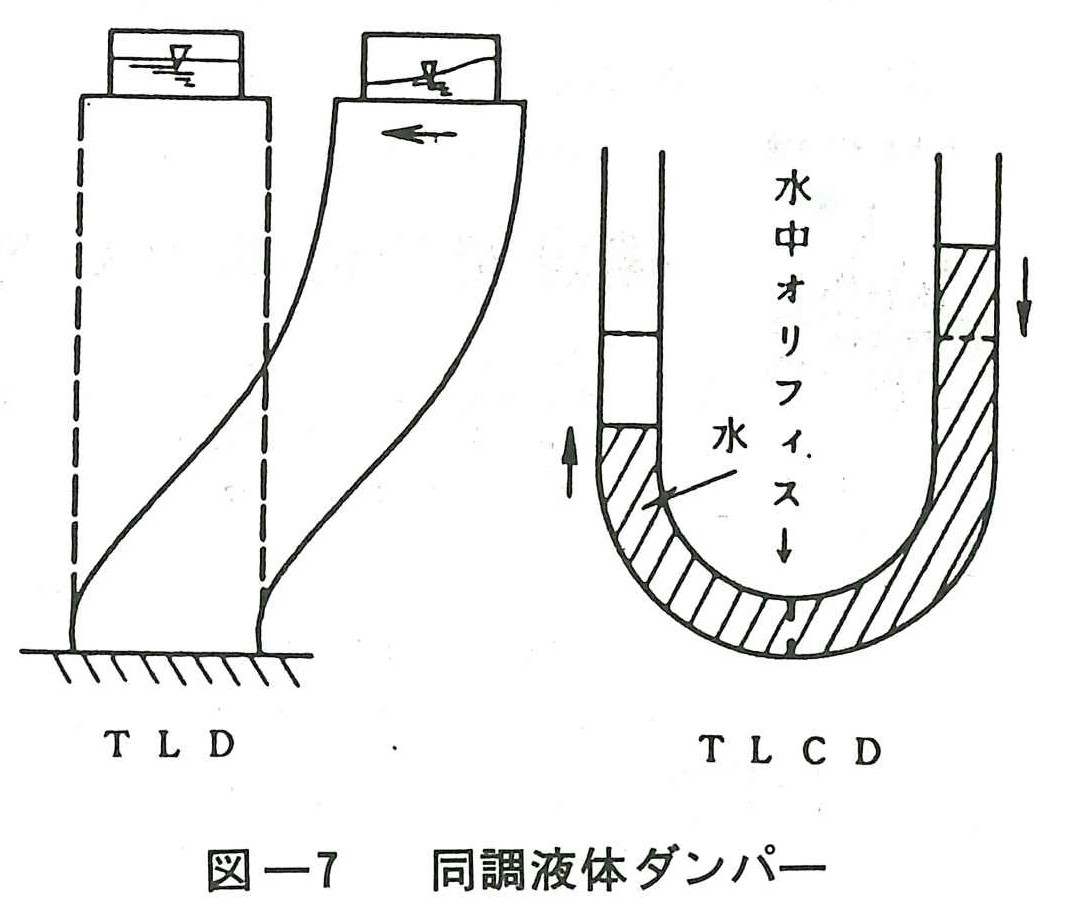
図ー7にこの装置の例を示すが,一般に自由表面をもつ液体の動揺振動を用いたものを同調液体ダンパー(Tuned Liquid Damper,略してTLD),U字管内の液体の振動を利用するものを液柱管ダンパー(Tuned Liquid Column Damper,略してTLCD)と称している。この装置の利点としては次のことが考えられる。
(1)微小振動に対しても確実に作動
(2)容器と水だけであるため経済的
(3)上下を除いた水平2方向の同時制振が可能
(4)個数は多いがそれぞれが小型容器に分かれているので,架設時などでも簡単に移動できる。
一方,TLDにおいても構造物系の質量に対して1%程度の質量を必要とするため,鉄の比重に比べて水の比重は約0.13と小さいことからTMDより大きなスペースを必要とする欠点もある。
TLDにおいてもTMDと同様に固有円振動数の同調および減衰が必要となる。TLDの液体動揺の固有円振動数は容器および水深の関係で決定できるが,TLCDにおいては管内の空気圧を変化させることで微調整できる。減衰を増加させる方法としては網ネット,水面上に発泡材の粒子を浮かべたり,水中オリフィスを用いるなど種々開発されている。
TLDは現在,斜張橋架設時の主塔の風による振動の制振装置として用いられたり,横浜マリンタワーのような展望塔において人体の不安感をなくすことを目的とした制振装置として利用されている。
3.2.4 インパクトダンパー
剛体の衝突運動を利用したものをインパクトダンパーという。この場合の制振子として鋼球を用いることが多く,制振子が安定した同期振動をする時に初めて制振効果が得られることから,制振子と壁の間の遊間距離dが重要なファクターとなる。この遊間距離は構造物系の固有円振動数や応答変位による影響が大きく,安定した制振効果を得るためには最適な値を決めなければならない。通常,遊間距離d=2~3mmであれば十分と考えられる。このインパクトダンパーの特徴としては1つの振動だけでなく,高次の振動に対しても有効に働くことである。
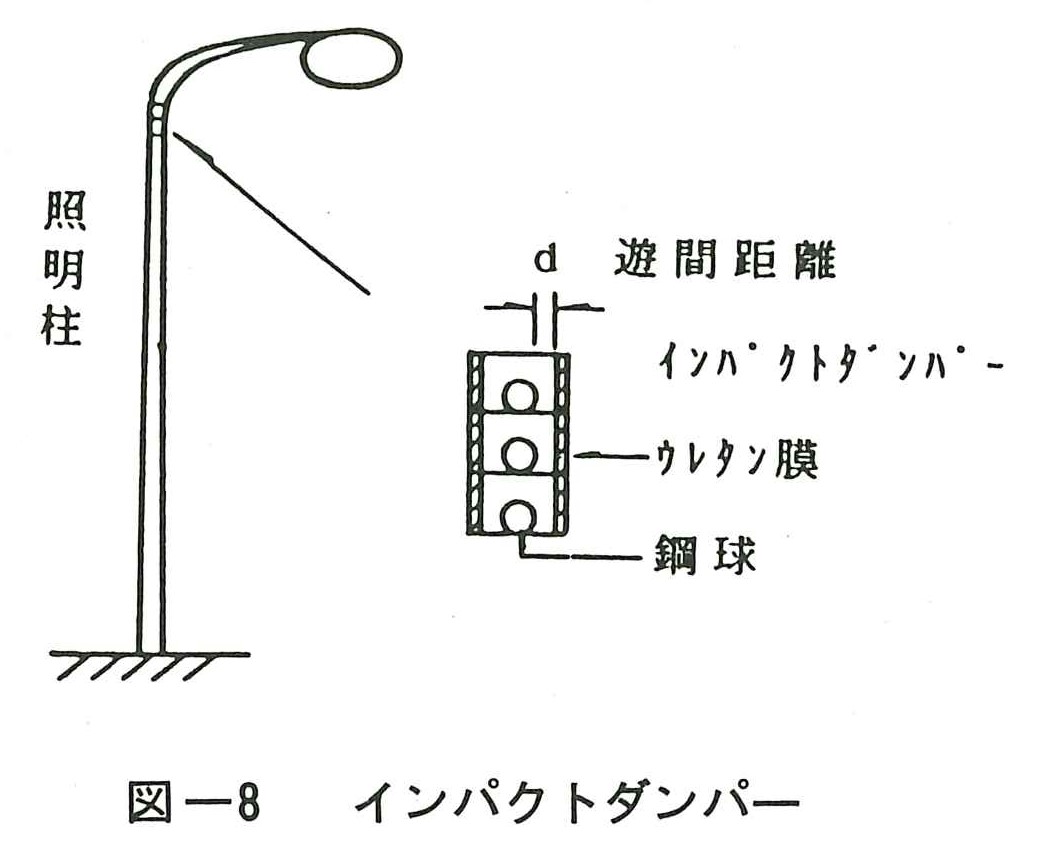
図ー8は照明柱の風による振動(カルマン振動)の制振用として,現在横浜ベイブリッジ等に用いられている装置である。制振子の構造物系の質量に対する割合は1~2%であれば十分であり,カルマン振動のようにある程度定常振動をする場合には有効である。この装置の欠点としては衝撃音が発生することであるが,内部にウレタン膜を施し,容器を密閉すればほとんど外部に音がもれることはない。この他に,剛体の代わりにチェーンや振り子などを用いたものがあり,実用化されている。
参考文献
(1) 振動制御コロキウム PART-A,構造物の振動制御,1991,7 土木学会構造工学委員会,振動制御小委員会
(2) 制振構造の電力施設への適用性に関する調査 松田泰治,電力中央研究所報告,調査報告,U91012,平成3年6月
(3) 土木振動学 小坪清真 森北出版




