ＮＡＴＭトンネルの施工では，地山の変状を予測しながら適切な措置を講ずる必要があり，そのために計測管理システムが導入されている。ところが硬岩地山の場合，地山の変形が非常に小さいため，精度ある計測を行うことが難しく，計測管理が有効に機能していないことが多い。最近では，計測値に変わるものとして，切羽観察を用いて最終内空変位の予測や支保の選定などを行う試みがなされてきている。そこで硬岩ＮＡＴＭでの変状の実態を把握するとともに，変状の発生の有無の予測に切羽観察を活用する方法について報告するものである。

ＮＡＴＭトンネル施工中には，切羽の肌落ちや崩壊，吹付コンクリートのクラックの発生やコンクリートの剥落，ロックボルトの変形，鋼製支保工の座屈などさまざまな変状が発生する。ここでは，硬岩地山に施工されたいくつかのトンネルに関する工事記録をもとに，変状の実態を統計的に調べるものである。

対象としたトンネルは，丹波古生層あるいは秩父古生層にＮＡＴＭにより施工された二車線の高速道路トンネルであり，岩質は粘板岩・砂岩・チャート・輝緑凝灰石に属するものである。幅員は８m～９m程度であり，施工法はおもにショートベンチ工法を採用している。なお解析に使用したトンネルの総延長はおよそ8,400mである。

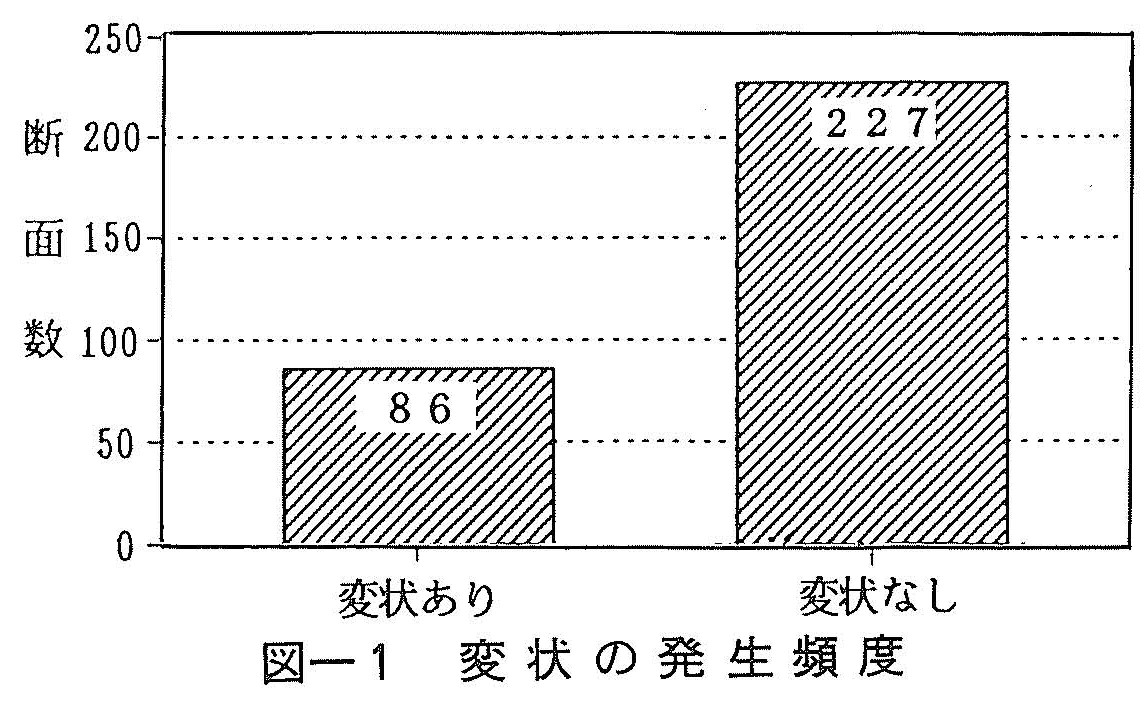
図ー１は変状の発生断面数の割合を示したものである。収集した断面は300断面ほどであるが，このなかで地山や支保工に変状が認められたものは86断面である。これは全体の27％にあたり，およそ100mにつき１回程度の割合で何らかの変状が発生したことになる。

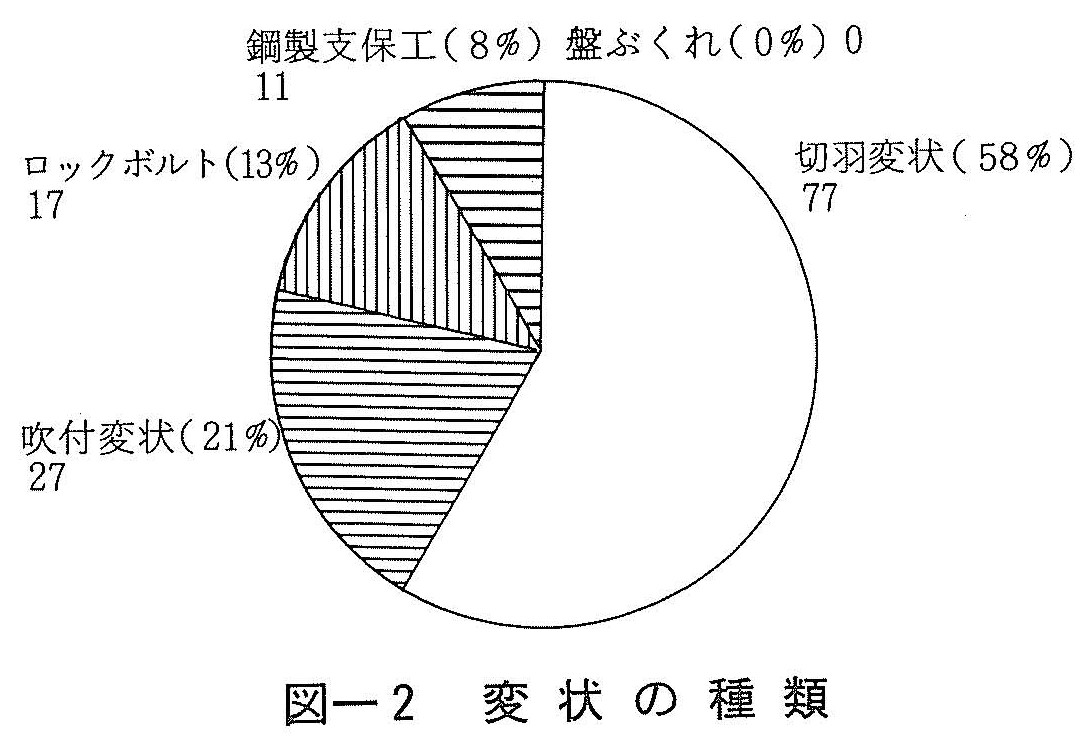
変状の内容はさまざまであるが，それらを大まかに分類すると図ー２のようになる。変状のなかでは切羽に関するものが最も多く，77断面で発生している。このことは切羽が掘削直後は無普請であることから当然のことといえる。ついで，吹付けコンクリートの変状が27断面で発生している。またロックボルトに関する変状は17断面で，鋼製支保工の変状は11断面でそれぞれ認められている。なお，データを収集したトンネルは，土被りにして30～300m程度であるが，硬岩であることから盤ぶくれは認められていない。

それではトンネルを構成する支保別にさらに細かい変状内容の発生傾向を調べてみることにする。

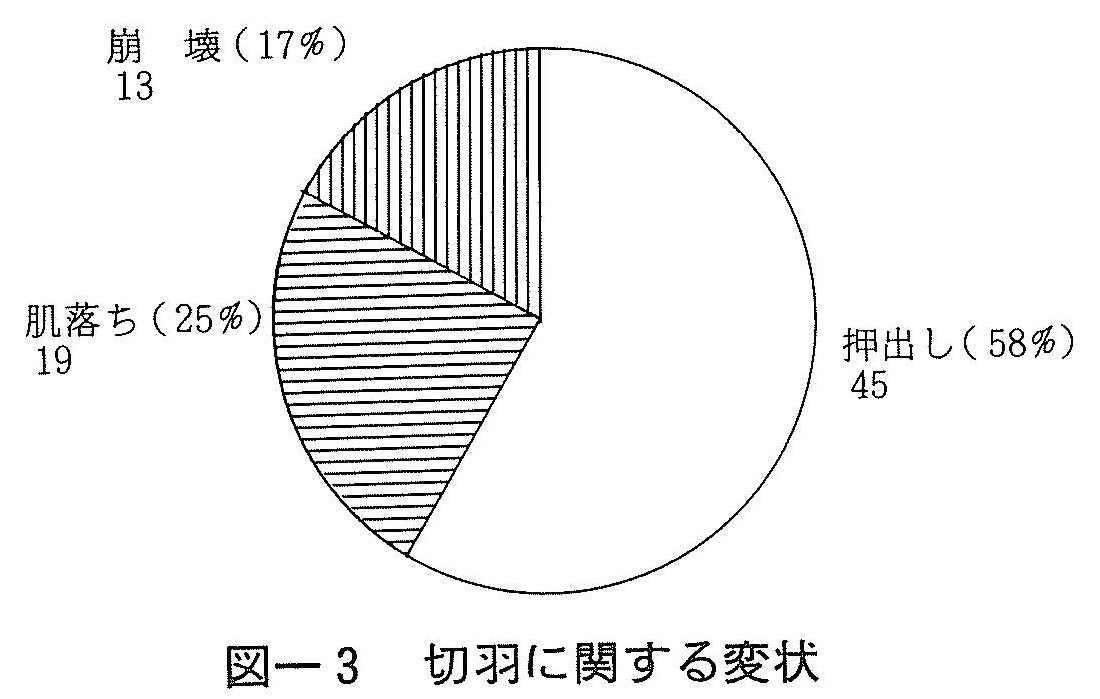
図ー３は切羽に関する変状の発生数とその割合を示したものである。切羽の変状に関しては，そのほとんどが押出しを示したり，あるいは肌落ちをした軽微な変状であるが，崩懐にまで至ったものも13ケースある。切羽の安定は施工上重要であるため，切羽に変状が発生した断面では，ほとんどの場合，斜めボルトを施して変状に対処している。

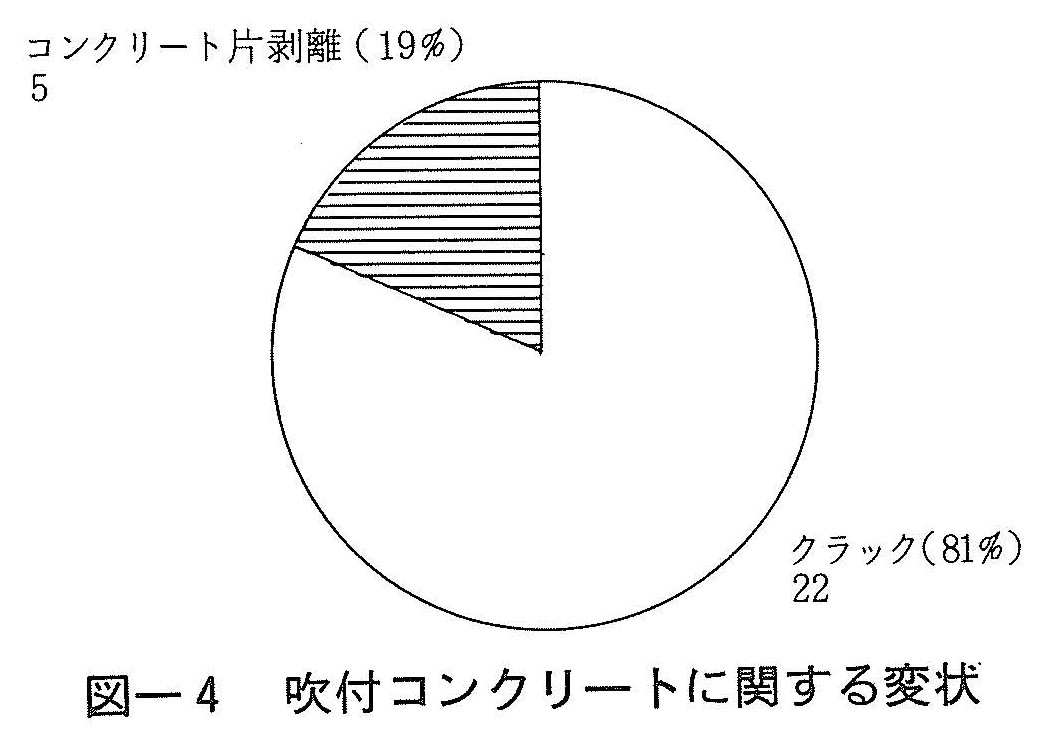
図ー４は吹付けコンクリートに関する変状の内容を示したものである。図によると，変状の大部分（22断面）がコンクリートにクラックが発生した事例である。また，コンクリートの剥落を生じるような深刻な変状も5断面で認められる。

また，ロックボルトの変状については，発生した変状17断面のすべてがプレートの変状であり，頭部が脱落したり，ロックボルトが破断するなどの変状は発生していない。

鋼製支保工の変状については，図ー５に示すように，支保工に変形を生じたのが６断面であり，さらに変形が進んで座屈した事例が５断面で発生している。

各トンネルの断面で発生した変状をその内容の組合せごとに分類すれば表ー１のようになる。なお表中の〇印はその変状が同じ断面内に存在することを示しており，逆に×印はその断面に該当する変状が発生しなかったことを表している。

実際に発生した変状内容の組合せは，タイプＡからタイプＨまでの８種類である。そのうち圧倒的に多いのが切羽のみの変状であるタイプＡであり，86断面中59断面を占める。これ以外のタイプとしては，切羽とロックボルト・吹付コンクリートおよび鋼支保の変状を内容とするタイプＨが７断面，吹付コンクリートとロックボルト変状からなるタイプＤが５断面，さらにタイプＤに切羽の変状が加わったタイプＧも５断面というようにいずれも事例は少ない。

また表より，吹付けコンクリート・ロックボルト・鋼製支保工の変状は，単独で発生することは少なく，多くの場合切羽の変状と同時に発生していることがわかる（タイプＣおよびタイプＥ～タイプＨ）。

前節では，変状をその内容の組み合わせごとに８種類のタイプ分類したが，タイプＡに属する断面数が59個と多いのに較べ，他のタイプは非常に少ないことから，変状の傾向がつかみにくい。そこで，変状が主として切羽に発生しているか，あるいは，吹付けコンクリートやロックボルトにも及んでいるかという２つの観点を導入することにより，変状のタイプを以下のように大きく３つの変状グループにまとめることとする。

このように変状を類型化することにより，変状の性質を，より具体的に把握することができる。すなわち，タイプⅠは変状が切羽のみに発生した場合であり，支保は安定でも，トンネルの切羽のみが掘削軸方向に押し出し，肌落ちをしたり，果てには崩壊した場合があてはまる。また，タイプⅡは，切羽はほぼ安定でも，ロックボルトや吹付けコンクリートに変状が多く発生した場合である。ただし，タイプⅡでは鋼製支保工が変状するまでには至ってない。一方，タイプⅢは３つの変状グループのうちでは，最も深刻な変状であり，切羽・吹付けコンクリート・ロックボルト・鋼製支保工の全体にわたって変状が発生したものである。

各変状グループの発生頻度は，タイプⅠが59断面で発生頻度が最も高く，変状全体の68％を占める。タイプⅡは11断面でしか発生しておらず，これは全体の13％である。また，最も深刻な変状であるタイプⅢは16断面で発生しており，19％にあたる。すなわち，変状が発生した断面のうち５断面に１回の割合で，全体的な変状が発生していることになる。これは掘進距離でみる，とおよそ500mに１回の割合である。

変状の発生と計測値あるいは観察結果との関連性について，資料に基づいて分析するが，そのまえに，現状の計測管理において，硬岩地山の変状を予測する際の問題点について簡単に述べておきたい（表ー２）。

前述のように，計測管理システムは硬岩地山では有効に機能していない場合が多い。その理由のひとつは，地山の変位量がわずかであるため，計測に関して十分な精度を確保することがむずかしいことであるが，それ以外にもいくつかの理由が考えられる。すなわち，計測に基づく情報は，すでに支保が施工され，数日の遅れをもって得られるため，結果が得られる頃には切羽も進んでおり，測定結果を施工にリアルタイムで反映させることがむずかしいことが挙げられる。また，計測には手間と費用がかさむため，能率の面を考えると，多くの測点がとれないことも，計測の活用をはばむ原因となっている。

一方，トンネルの施工現場では，従来より切羽観察が行われているが，切羽の観察結果は，すべての掘削断面において即時的に得られ，不連続性を表す指標も多く含まれている。ただし，計測結果が客観的データとして定量的に把握できるのに較べ，切羽観察は定性的なデータでしか得られないため，計測管理に活用しにくいという欠点がある。しかし，数量化理論やファジィ理論を用いて，定量的なデータに変換することにより，切羽観察も計測値と同様の扱いをすることが可能である。また，観察内容を簡略化し，記録方法をカテゴリー化することで，主観の入り込む余地を少なくすることができる。

そこでここでは判別分析や数量化理論を用いることにより，計測値と切羽観察結果のいずれが変状発生の予測に有効であるかを調べるものである。

ＮＡＴＭにおける計測管理ではさまざまな内容が計測される（表ー３）。その中で地山変状を推測する上で重要であり，かつ比較的簡単にしかも精度よく求められるものは，内空変位量，天端沈下量および変位速度の3つである。また事前あるいは施工中に得られる情報のうち，地質条件を表すものとして弾性波速度を，外力の大小を表すものとして土被り厚さを同時に考えることとする。

本節では，前述の変状のうちいずれかが発生する状況を地山変状有り，いずれも発生しない状況を地山変状なしと定義して，判別分析により変状の有無を予測するものである。まず計測値の変状予測に関する有効性を調べるために，変状の発生の有無を外的基準とし，上述の計測値３変量と弾性波速度・土被り厚さを説明変数として判別分析を行った。結果を表ー４に示す。

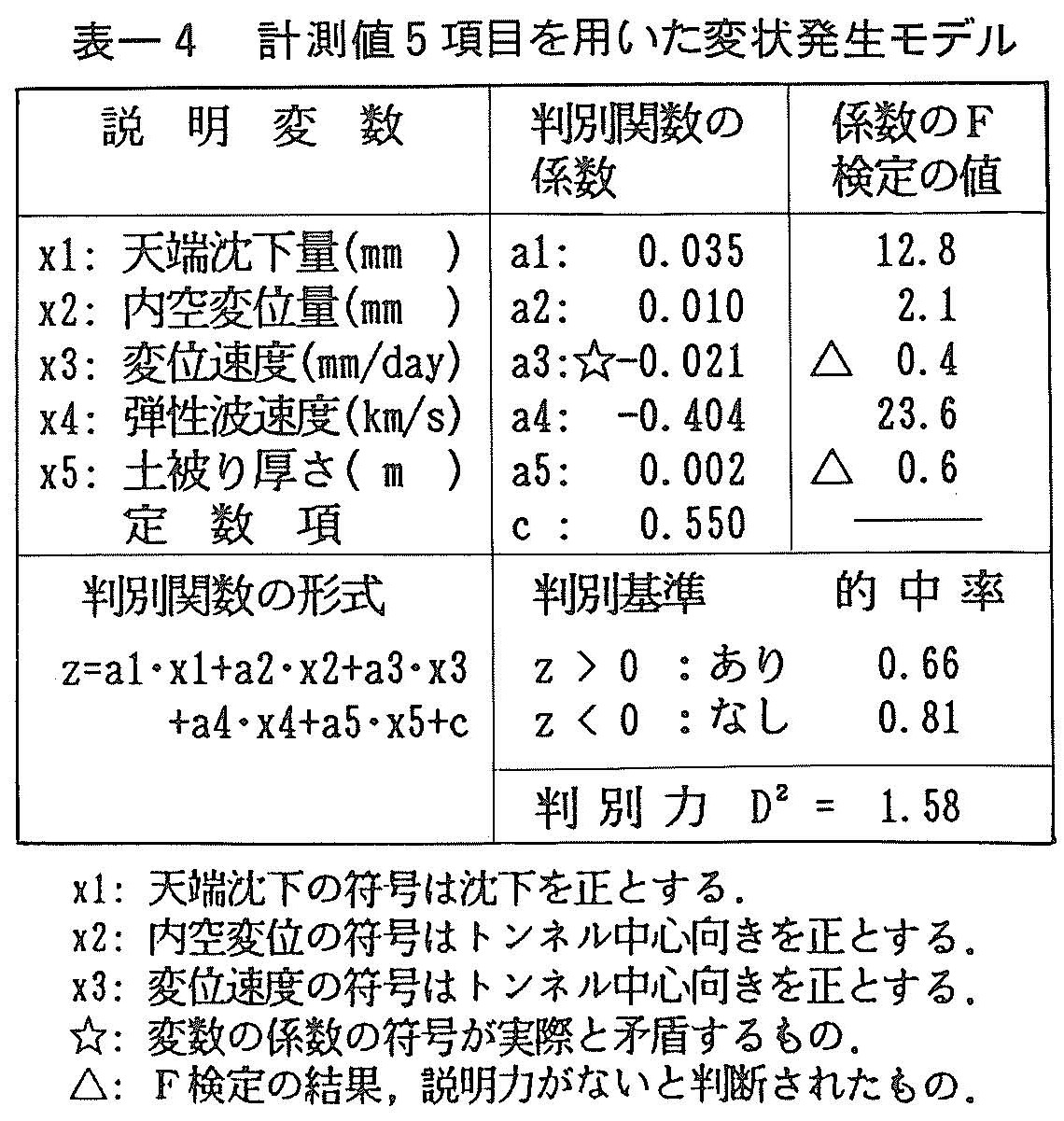
本表のＦ検定の値は，この値が大きい方が変状の判別に説明力を持つことを意味し，逆に小さいと変状の発生との関連性が小さいことを意味するが，弾性速度と天端沈下のＦ値が大きく，変状の予測に有効な変数であるといえる。逆に，内空変位・変位速度・土被り厚の３変量はそれほど変状の予測に役だっていないことがわかる。変数の有効性をＦ＝2.0を基準にしてみれば，表中に△印を付した土被り厚と変位速度は判別予測に有効ではないといえる。また，本表において☆印を付した変位速度は，実際の現象に照らして，判別関数の符号に矛盾が生じている。なお，表中の判別力Ｄ^２は２群の平均値間の標準化距離であり，判別分析における判別の良さを示すものである。

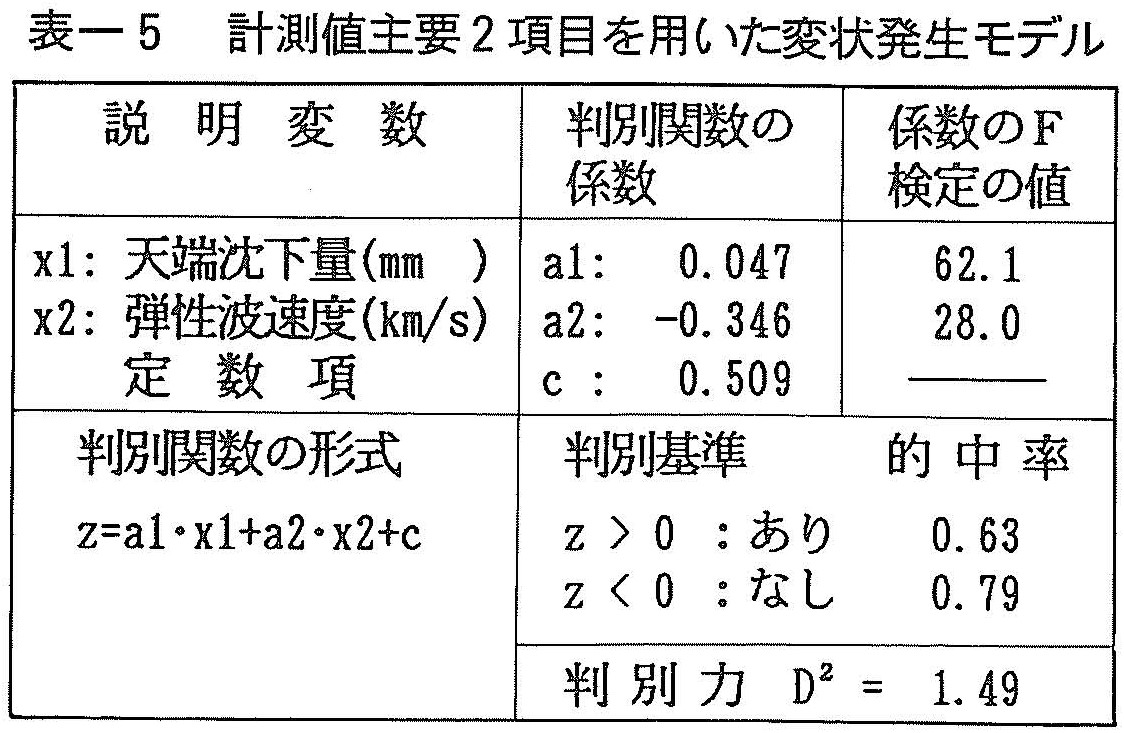
以上の考察をもとに，寄与が高い上位の２変数のみを説明変数とし，判別分析を再度行えば表一５のとおりである。本表と表ー４とを比較すれば，本表の場合は判別力Ｄ^２がやや低下し，的中率も小さくなっていることがわかる。しかし，判別関数の係数のＦ値は全て2.0以上であり，しかも，実際現象と符号のうえでの矛盾は生じていない。

本モデルでは，計測値として採用されるのは天端沈下のみであり，この点従来の計測管理でスプリングライン付近の相対量としての水平内空変位を主体としてきたことと異なるといえよう。すなわち，本例は数本のトンネルの施工実績をもとにしたものであるため，必ずしも断言できないが，中古生層の硬岩地山では，水平内空変位を主体とする計測管理では変状の予測はむずかしく，むしろ天端沈下の測定精度を高め，絶対量としての天端沈下を主体とする計測管理に変えることが必要であるものと判断される。

各現場で用いられた切羽観察シートから，観察項目をひろいだせば表ー６の各項目を挙げることができる。本表は，地質条件，岩盤強度，割れ目，湧水などに関し，可能な観察が網羅されている。なお，この表中のカテゴリー区分は一般に用いられているものより簡略化されている。

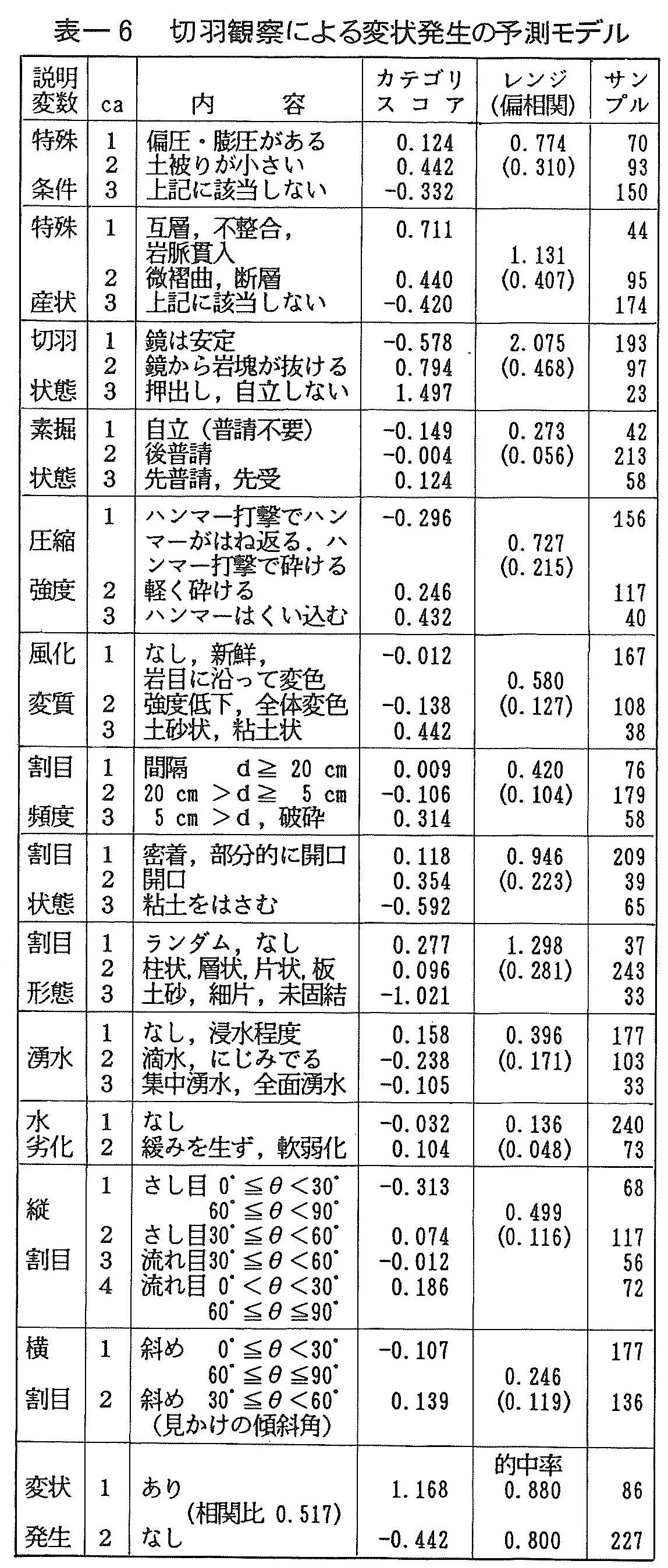
これらの観察項目を説明変数として，数量化理論第Ⅱ類を適用することにより，変状の発生を予測することができる。表ー６の右側にそれぞれの説明変数のカテゴリースコアを示す。変状の有無を予測するには，表に示す各項目について観察を行い，該当するカテゴリースコアを足し合わせることにより判断する。もしその合計値が正であれば，変状が発生する可能性が大きいことを意味し，逆に負であれば，変状が発生しないことを意味する。モデルの的中率は80％以上であり，十分な精度を有するといえる。この結果を，計測値を用いた場合（表ー４あるいは表ー５）と比較するならば，切羽観察を用いた本例のほうがわずかに予測精度が勝ることがわかる。

本モデルでの主要な説明要因は，レンジおよび偏相関係数で判断すれば，切羽の状態・割目の状態・割目の形状などであり，岩の不連続性に関する項目が判別に大きく寄与していることがわかる。これは硬岩地山の場合，地山を構成する個々の岩石自体は非常に高い強度を有するが，地山全体の強度は割れ目の頻度や状態に影響されることを表していると考えられる。

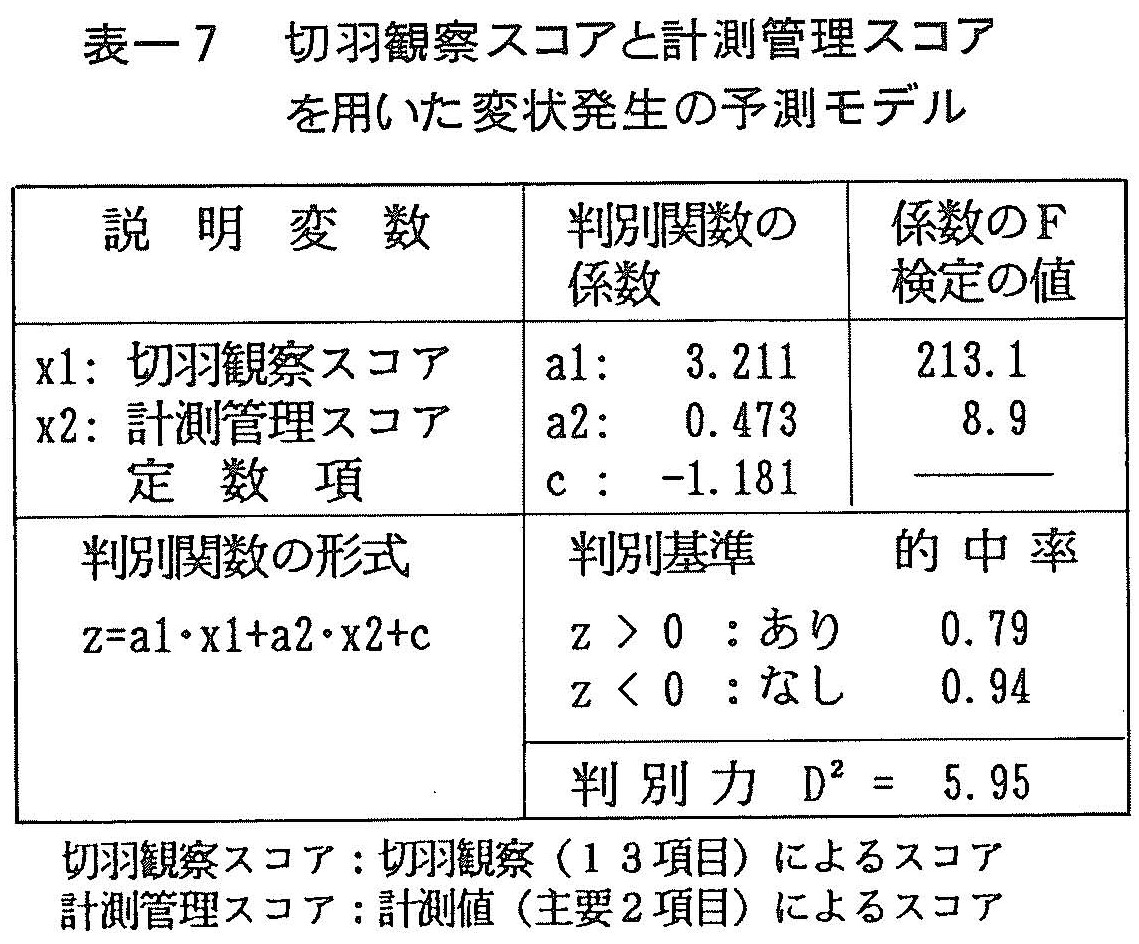
変状の有無の予測について，切羽観察および計測値のそれぞれを用いて検討を加えたが，精度をあげるために，切羽観察と計測値の双方を使って評価することが考えられる。すなわち，切羽観察の判別スコアと計測値の判別スコアをそれぞれ説明変数として，判別分析により変状の有無を判別した。表ー７に分析結果を示す。表ー５に較べて判別力Ｄ^２が大きくなり，判別モデルがより適切になったことがわかる。

また，本モデルにおける係数のＦ値を比較してみると，切羽観察のＦ値が計測値のＦ値よりも著しく大きく，中古生層の硬岩地山では，切羽観察のほうが変状の発生の予測に有効であるということがわかる。逆に計測値の寄与は小さく，切羽観察の結果を，地山条件に応じて補正する程度の意味しか持たないといえる。

本研究は変状の実態を把握するとともに，変状の発生を予測する手法を提案するものであるが，切羽観察のみを用いることにより，あるいは，切羽観察と計測値を併用することにより十分な精度を有するモデルが作成できた。本法は地山の観察に力点をおくものであるが，分析結果からみても，切羽観察が地山の変状の予測に有効であることがわかる。また，本法は内空変位などの計測値のみによる方法に比べて予測精度が高く，しかも結果を定量的に把握できるなどの実用性を備えている。

以上のように，中古生層の硬岩地山におけるトンネルの施工では，切羽の観察が変状の予測に有効であり，現状の計測のみでは十分な予測はできないことが明らかにできた。このことは，今日のＮＡＴＭの施工において，周辺地山の挙動の把握方法として，計測を最優先させる傾向があることに反して，観察という最も初歩的な作業が重要であることをあらためて認識させるものである。