軽打法による場所打杭の支持力推定
九州大学工学部土木工学科
助教授
助教授
烏 野 清
九州大学工学部土木工学科
大学院生
大学院生
麻 生 稔 彦
九州大学工学部土木工学科
教授
教授
堤 一
日本道路公団東京第一建設局
課長代理
課長代理
前 田 良 刀
㈱建設技術研究所福岡支社
次長
次長
松 井 謙 二
1 はじめに
近年,都市域における基礎工法として,騒音・振動を低く抑えることができる場所打ち杭工法が,多く用いられるようになってきている。しかし,杭の支持力管理という観点から見てみると,場所打ち杭には多額の費用と労力を必要とする静的載荷試験が行われているのみであり,簡便な支持力推定法の開発が強く望まれている。一方,打込み杭については,静的載荷試験に代わり波動理論の応用による動的支持力推定法の研究が進み,一部は実用に供せられるようになってきている。この打込み杭について用いられている動的推定法は,ハンマーリバウンド量や貫入量等をパラメーターとして用いるため,直接場所打ち杭へ応用することは困難である。そこで,本論文は場所打ち杭に対する簡単な打撃試験より,支持力を推定する方法を提案するものである。なお,この推定法の有効性は,静的載荷試験結果と比較することにより確認している。
2 支持力推定法
本提案法は動的試験を行うものの,その解析法は衝撃力と杭変位の関係を用いることから,基本的には静的載荷試験と同様な解析方法である。図ー1は提案した支持力推定法の手順である。以下に各項目ごとに説明する。
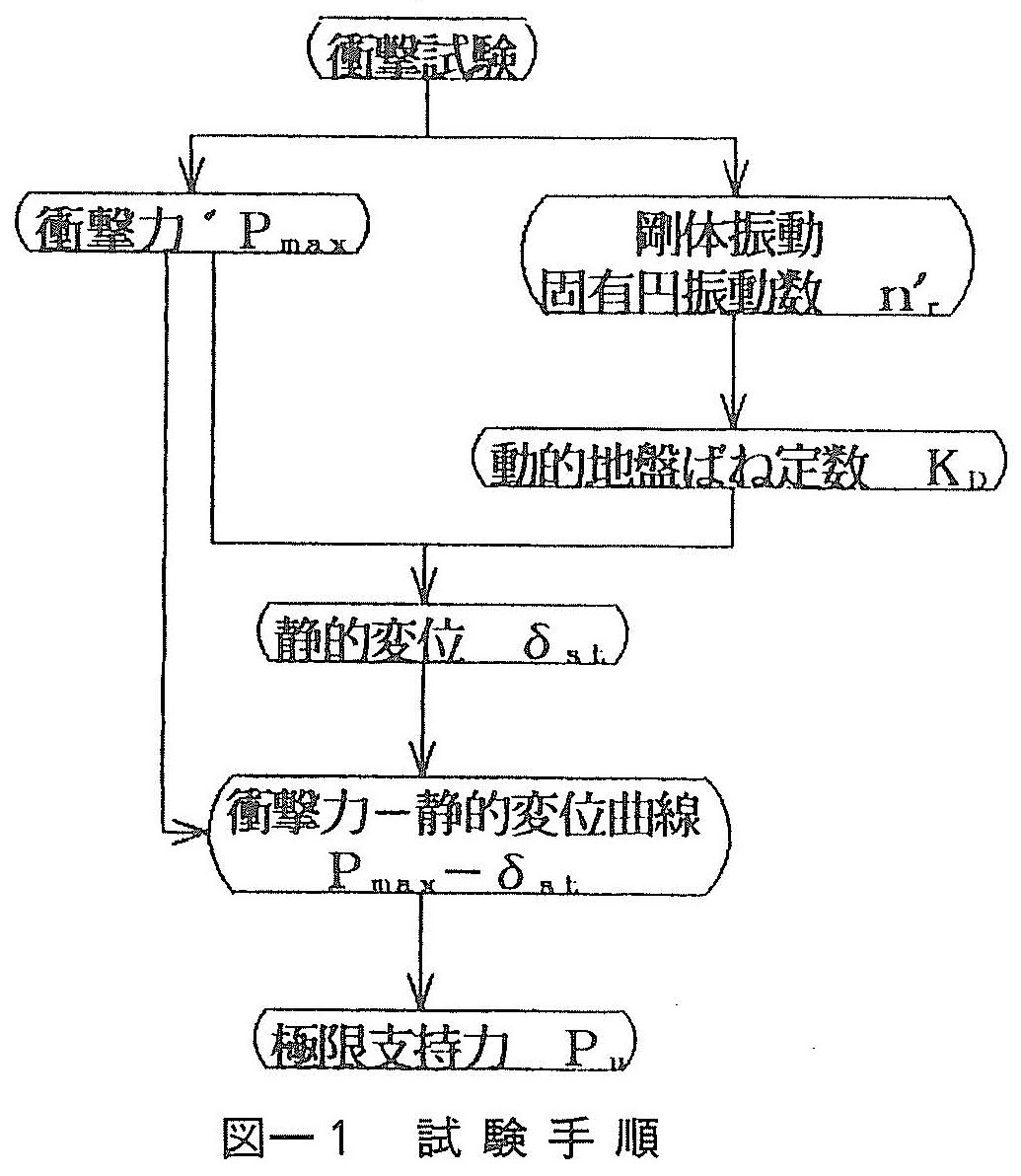
2.1 衝撃試験
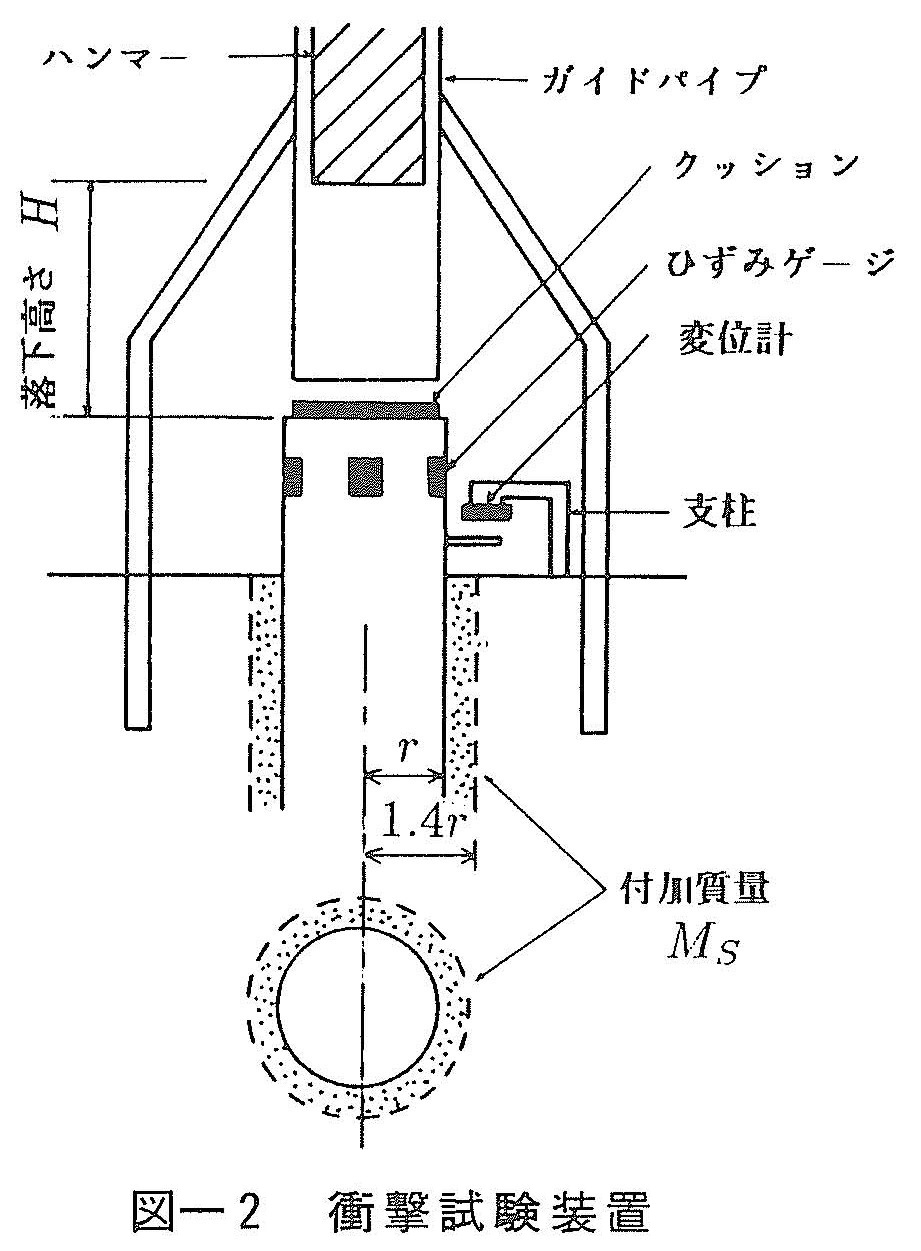
図ー2に衝撃試験の方法を示す。場所打ち杭上にガイドパイプを設け,この中を重量1.0~2.0tのハンマーを,クレーンにより所定の高さまで吊り上げた後,自由落下により杭を衝撃加振する。ハンマーの最大落下高さは杭の支持力により異なるが,試験の安全性から見て,およそ4mが限度と考えられる。この最大落下高さまで10~25cm間隔で落下高さを変化させて衝撃試験を行う。なお,打撃時に杭頭の損傷を防ぐためのクッション材としては,衝撃力の安定性を考えた場合,ゴム製より木製のものが良い。
打撃による杭の衝撃力と動的挙動を観測するために,杭頭においてひずみと変位を測定する。杭頭ひずみは偏心打撃の影響をかなり受けることから,1/4円周ごとに4点で測定し,それらの平均値を解析に用いる。また,杭頭加速度を2回積分して求めた杭頭変位は誤差が大きいことから,非接触型変位計を用いて変位を直接測定する方が良い。解析のためにデータをAD変換する場合,衝撃力の平均作用時間が4ms程度であることから,サンプリング間隔としては0.1ms程度が適当と考えられる。
2.2 衝撃力
図ー3に示す各落下高さごとの最大衝撃力Pmaxは,測定された最大杭頭ひずみεmaxを用いて,次式より求めることができる。

(1)式の動的弾性係数EDは鉄筋コンクリートからなる杭を一様な材質に置換したときの値であり,ひずみの時刻歴より求められる衝撃波の伝播速度Cを用いて,次式により計算できる。

Cは材質により異なるが,場所打ち杭では概ね4,000~5,000m/sの範囲であり,ρを0.255t/m3と想定した時に,EDは4.08×106~6.34×106 t/m2程度の値となる。
2.3 剛体振動の固有円振動数
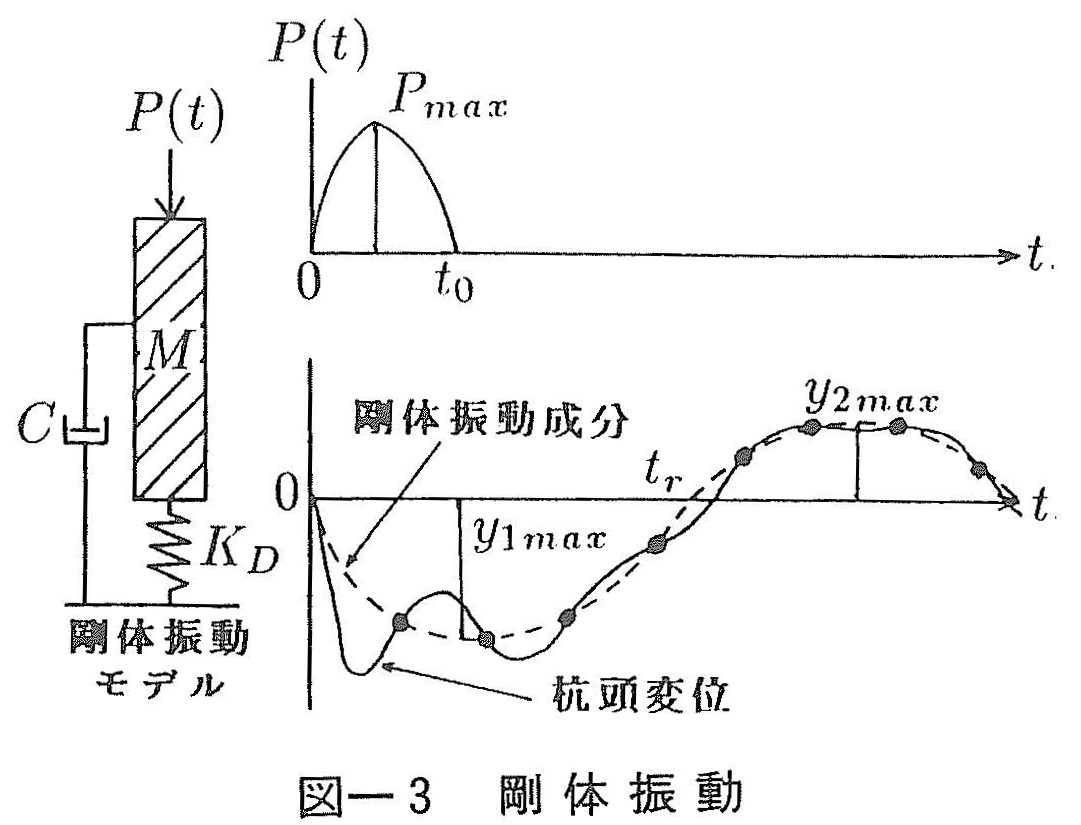
一般に,杭頭で観測される変位には図ー3に示すように,地盤ばねで支持された杭が一体となって振動する剛体振動と,衝撃力による波動が杭体内を伝播するために生じる伸縮振動の2つの成分が含まれている。これらの成分の中で,伸縮振動は衝撃力の波形および杭長に大きく影響されるが,杭支持力との関係は少ない。一方,剛体振動は地盤ばねに支持された振動系と見なせることから,杭支持力の影響を強く受けている。したがって,本推定法では衝撃力が大きくなるにつれて動特性が変化する剛体振動を用いて支持力を推定することとした。
通常,剛体振動は杭頭変位から計算で求めた伸縮振動成分を差引くことにより得ることができる(文献1)~3)参照)。しかし,場所打ち杭の場合には,図ー3に示すように伸縮振動のゼロ点(●印)を結ぶことにより,簡単な作図で剛体振動成分を求められることが多い。
この剛体振動は図ー3に示す1質点系にモデル化されることから,剛体振動の変位yrを用いて振動方程式は次式で表される。

Mは杭本体の質量Mpと杭と一体となって振動する杭周面の土の質量(付加質量)Msの和である。

実験結果によれば,場所打ち杭の付加質量は杭が排除した土の質量にほぼ等しく,これは杭および地盤の平均的な単位体積重量で考えると,図ー1に示す範囲の土が杭と共に振動していることになる。

(4)式におけるnrはhr=0の場合の剛体振動の固有円振動であり,減衰がある場合の固有円振動数nr´は次式より得られる。


このnr´は衝撃力が大きくなるにつれて,地盤の非線形性の影響を受け,徐々に小さな値へと変化する傾向を持つ。
2.4 動的地盤ばね定数
(4)式に示す動的地盤ばね定数KDは,杭先端および杭周面に働く地盤ばねの両方を含んだものである。このKDは実験より得られたnr´と(5)式に示すMを,(4)式に代入することにより得られる。
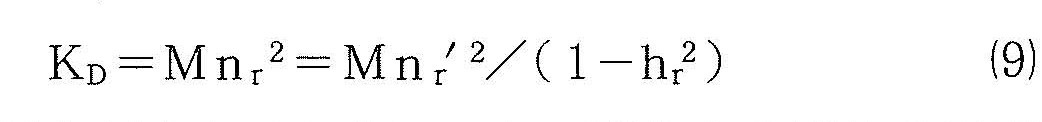
衝撃力が大きくなるにつれて変化する剛体の固有円振動数nr´を用いて,(9)式は動的地盤ばね定数KDの変化が計算できることを示している。
2.5 静的変位
衝撃試験より得られた剛体振動変位は,衝撃作用時間t0と剛体振動の固有周期Trおよび減衰定数hrの関数である動的応答倍率の影響を強く受けている。一般に,t0に比べてTrがかなり大きいことから,動的変位はPmaxが静的に作用した場合の変位に比べて,非常に小さな値となる。支持力を精度良く推定するためには,この動的応答倍率の影響を除く必要があることから,PmaxとKD を用いて,静的変位δstを次式の計算より求める。

2.6 衝撃力ー静的変位曲線
静的載荷試験により杭の支持力を求める場合には,載荷荷重と沈下量の関係を用いる。本法においても,同様にハンマーの各落下高さごとに得られた衝撃力Pmaxと,静的変位δstとの関係より極限支持力を推定する。
杭の静的載荷試験より支持力を推定する方法は種々提案されているが,そのほとんどが作図による方法であるため,人為的誤差が含まれることが多い。そこで,本法はPmax-δstの関係を次式に示すワイブル型の関数に近似することにより,主観の入らない推定を行うことにした。(文献10),11))

(11)式における,変位指数mは静的載荷試験では1.0として良いとの報告もあるが,本法に用いる場合には,動的と静的とでは地盤特性が多少異なると考えられることから,Pu,δy,mを未知数とした非線形最小自乗近似を行うことにした。
3 現場試験
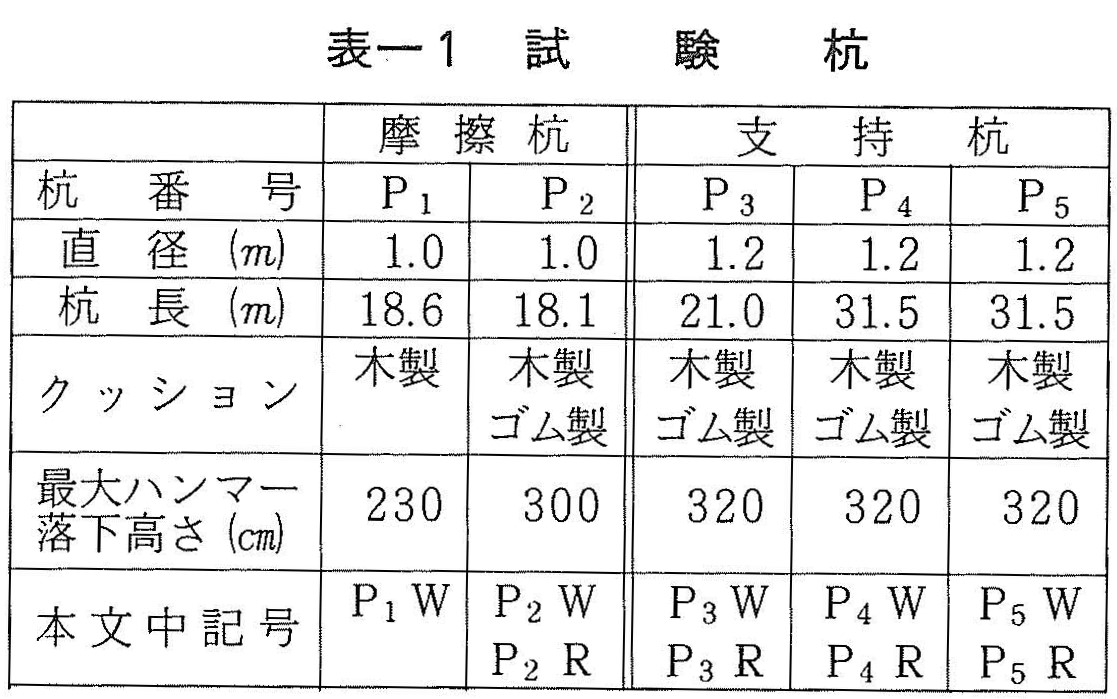
支持力推定法の妥当性を検討するために,2地点,計5本の場所打ち杭について衝撃試験を行った。表ー1に各杭の形状を,図ー4に各杭設置地盤のN値分布を示す。P1,P2杭は九州横断自動車道鳥栖J.C.T.~小郡I.C.間の基礎杭であり,これらの杭については静的載荷試験も併せて実施した。P3~P5杭は岡山市内の山陽自動車道の基礎杭である。これらの試験杭のうちP1~P2杭は摩擦杭として,P3~P5杭は支持杭として設計・施工されている。現場における試験の実施状況を写真一1に示す。

3.1 衝撃力
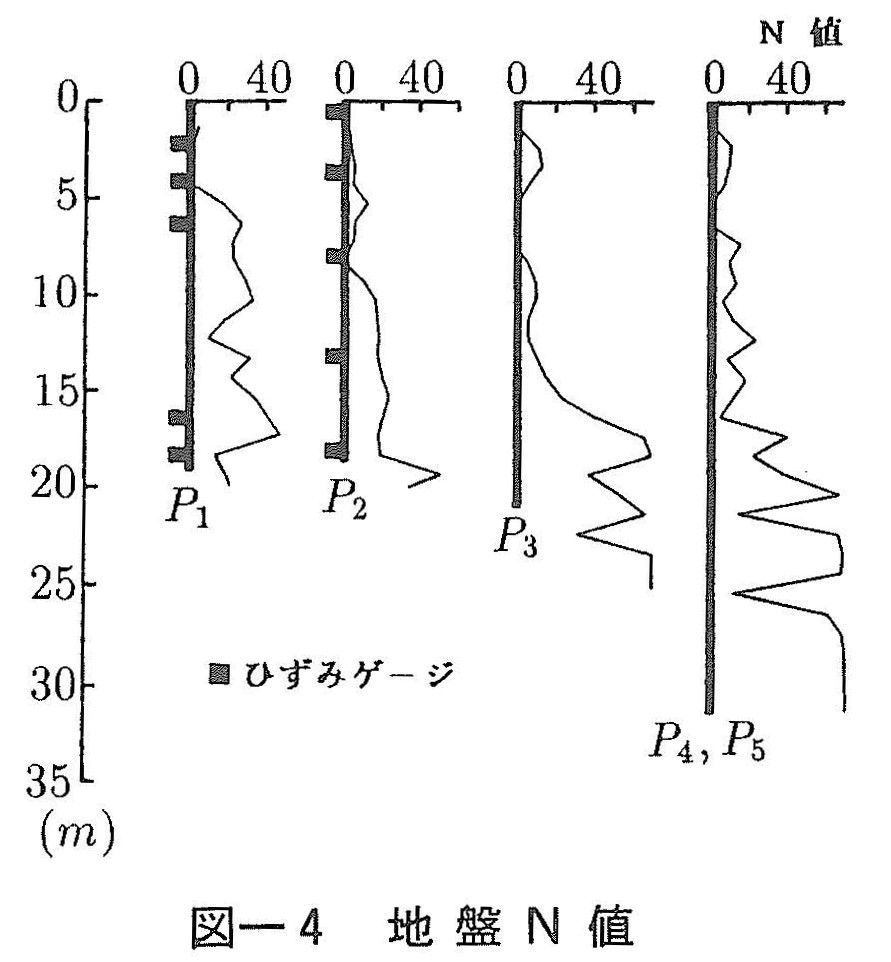
(1)式より求めた,ハンマーの落下高さと衝撃力の関係を図ー5に示す。図より同一落下高さにおいても杭およびクッション材により,衝撃力が異なることがわかる。本提案法では,杭周辺地盤ばね定数の変化を求めることが重要となることから,この変化が発現するために十分な衝撃力を与える必要がある。したがって,効率良く試験を実施するためには,あらかじめ落下高さと衝撃力の関係が明らかであることが望ましい。そこで,ハンマー,クッション,杭体間の波動関係を用いて衝撃力を求めると次式となる。(文献12))

(12)式を用いて各落下高さにおける衝撃力を求めると,図中の実線および破線となる。これらはいずれも実測値を良く近似しており,現場試験を行う場合の参考となろう。
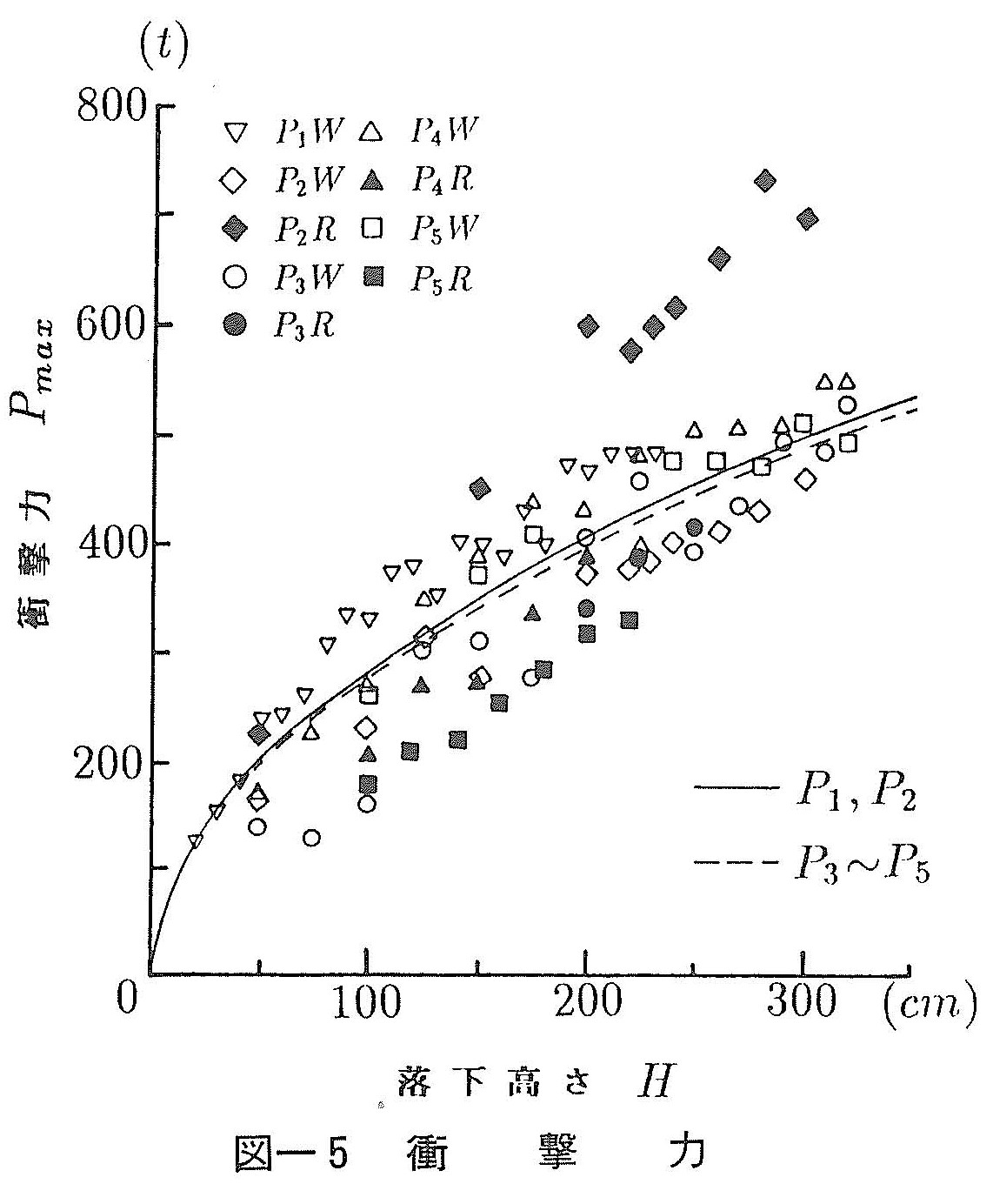
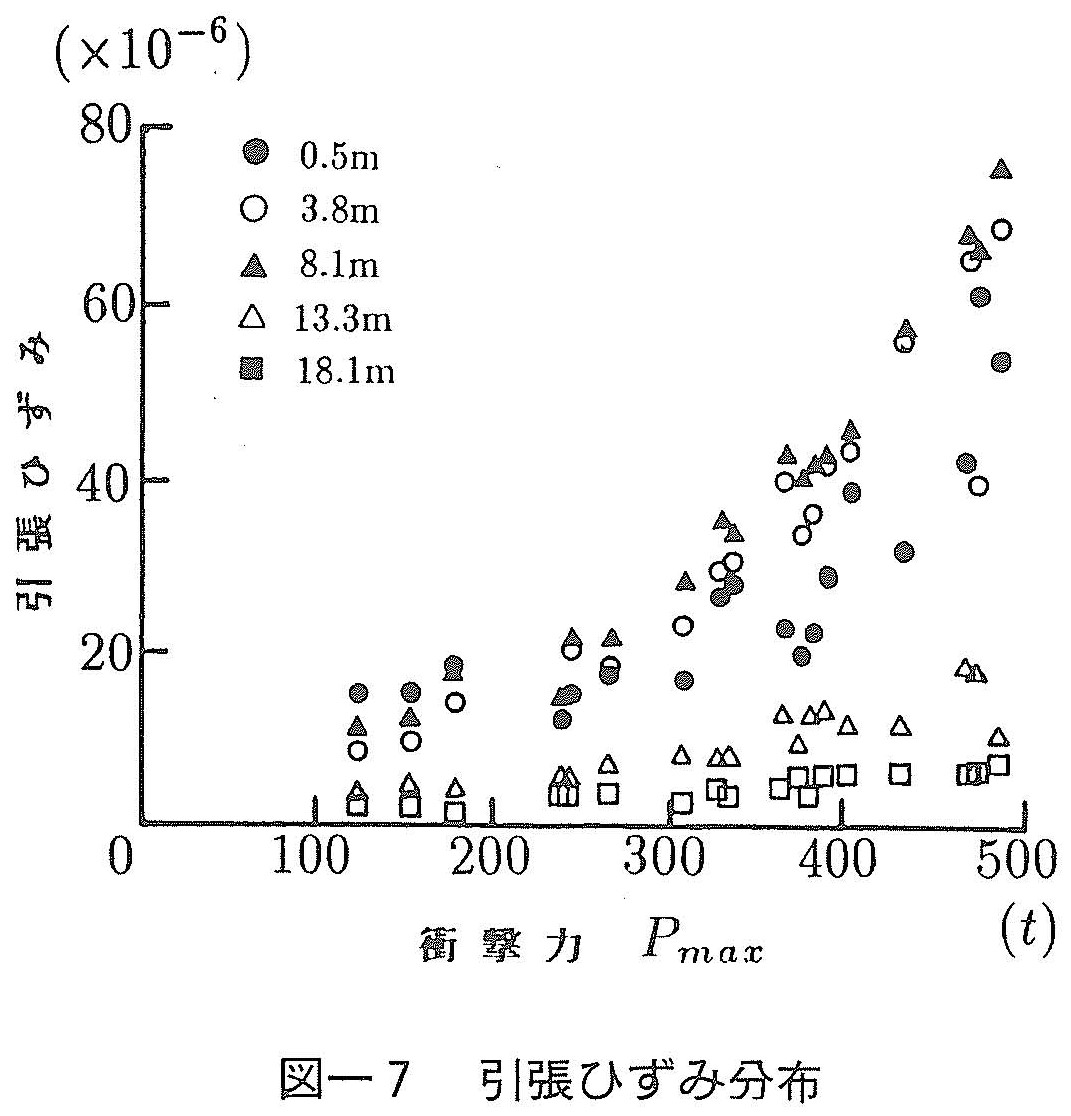
いま,場所打ち杭を打撃することにより生じた衝撃波は杭体を下降し,杭先端で反射した後に引張波として上昇する。コンクリート杭では,この引張力が杭体に亀裂を発生させる可能性があるため,引張力についての検討を行った。図ー6にP1~P5杭の杭頭で測定された最大入力圧縮ひずみに対する最大引張ひずみの比を示す。図よりP1杭の値がP2,P4,P5の各杭に比べて,著しく大きいことがわかる。摩擦杭であるP1では杭と杭先端地盤のインピーダンスがかなり異なるために,衝撃波の反射率が大きくなっているものと考えられる。また,支持杭とされるP3杭においても,P1杭に近い傾向が見られる。一方,P2杭は摩擦杭とされているものの,杭先端から地盤への応力波の逸散が大きく,P4,P5杭と同様に支持杭に近い状態にあると考えられる。そこで,P1杭における杭の深さ方向の引張ひずみ分布を示すと図ー7となる。杭体中央部(杭頭より8.1mの深さ)に発生した引張ひずみは80μ程度であり,杭頭で測定された値の約1.5倍となっている。
以上より,ハンマー重量や落下高さをむやみに増加させることは,杭体を破壊する恐れがある。特に,摩擦杭に対する試験においては事前に十分検討を行うと共に,試験中にはひずみを常時モニターする必要があろう。
3.2 杭の振動
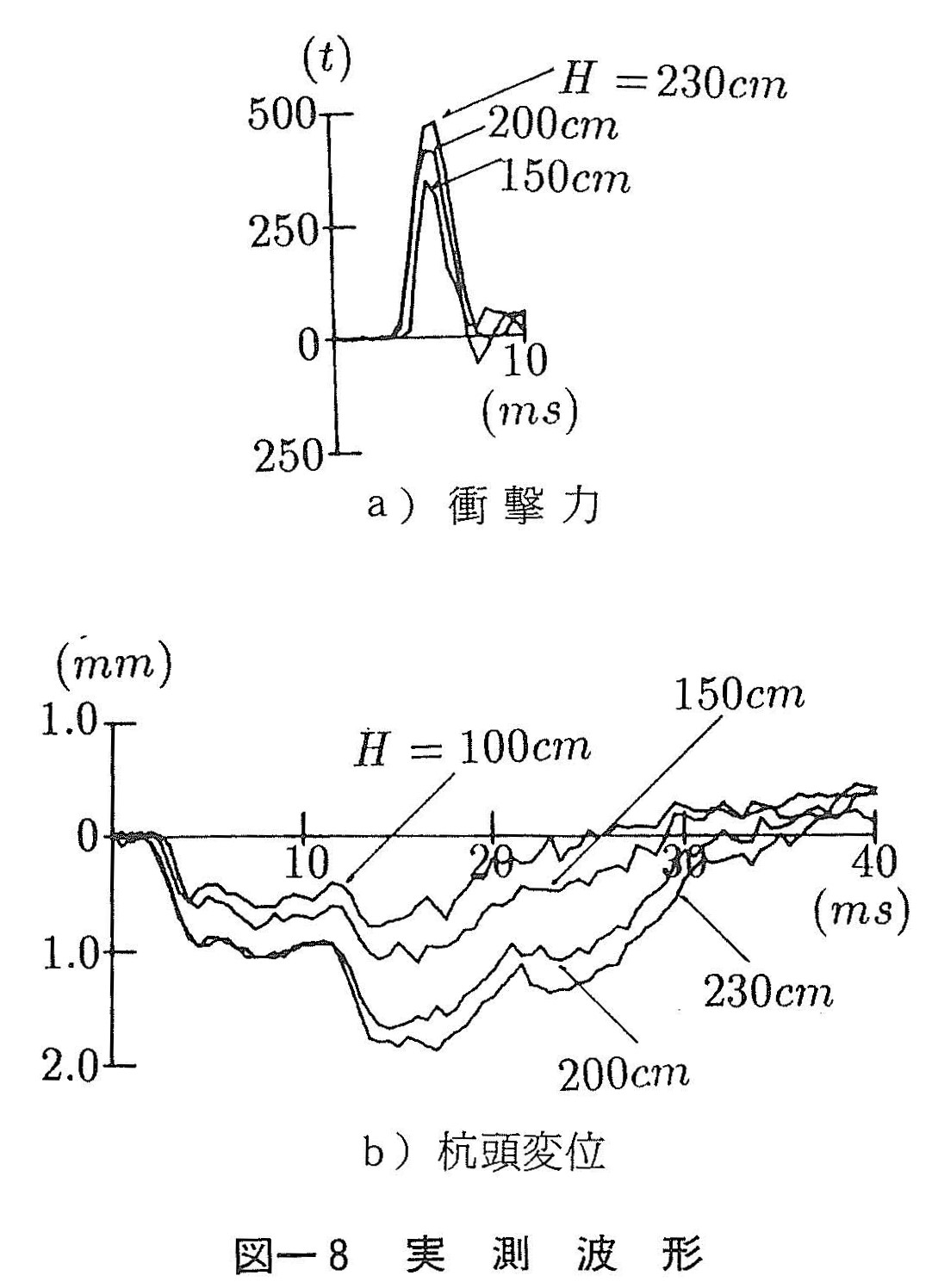
P1杭の代表的落下高さにおいて測定された衝撃力と杭頭変位の時刻歴を図ー8に示す。ハンマー落下高さが増すにつれ,変位および振動周期が大きくなることがわかる。この変化は杭周辺地盤の地盤ばね定数が,衝撃力の増加により軟化するために発生するものと考えられる。
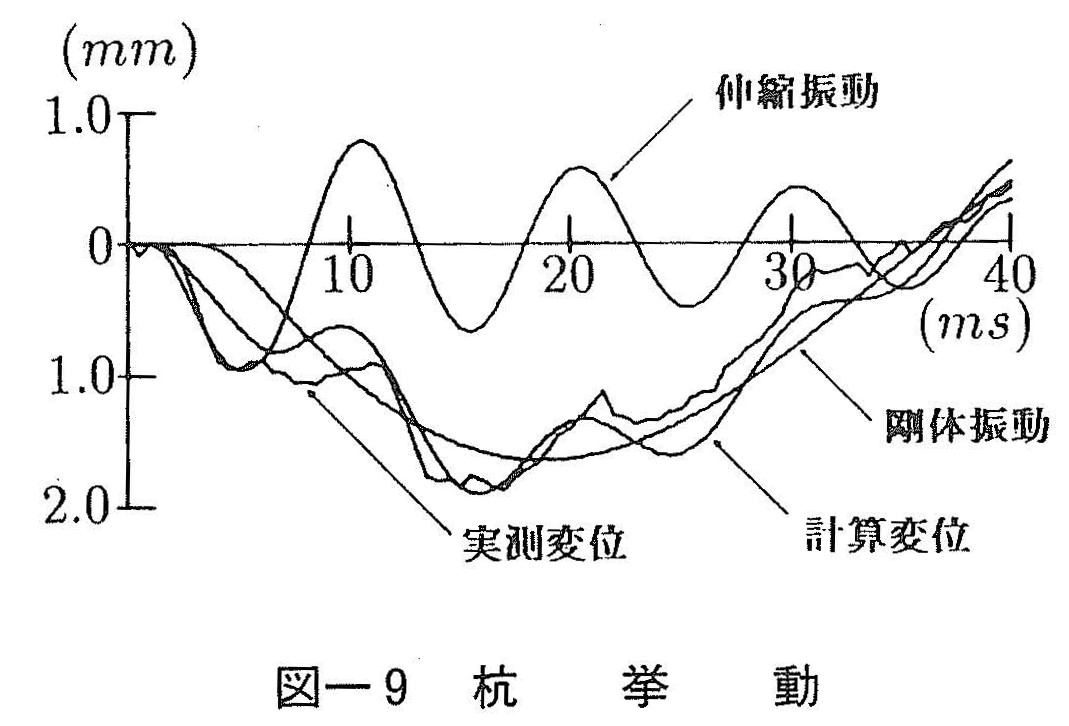
図ー9は計算により剛体振動と伸縮振動をそれぞれ求め,実測値と比較したものである(文献1)~3)参照)。この計算では,杭全体の伸縮量の1/2が杭頭に現れると仮定し,剛体振動変位に加えている。杭頭変位は図ー3で示したように剛体振動と伸縮振動とから成ることがわかる。また,実験値と計算値は良く一致しており,杭の動的挙動を正しく把握できたものと考えられる。
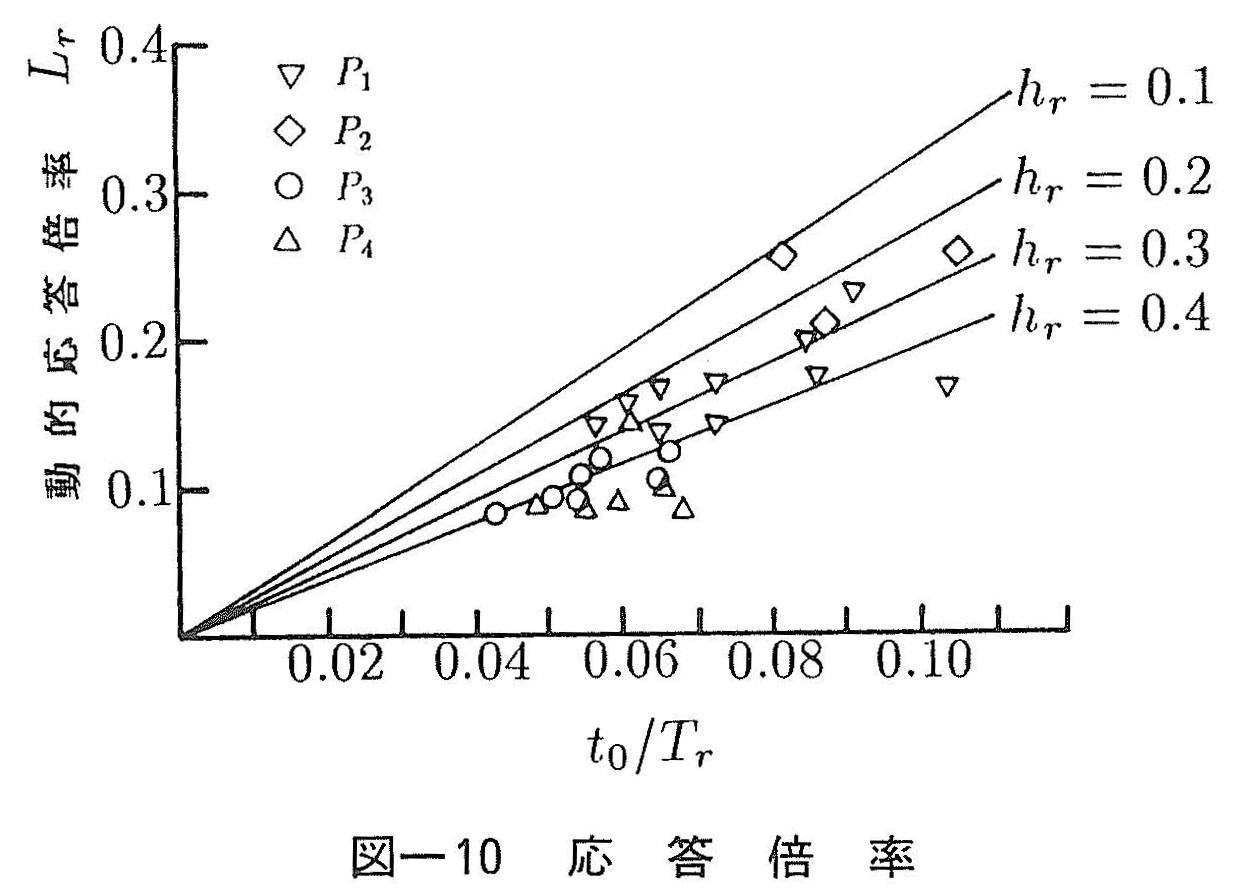
次に,応答倍率Lrの影響を検討するために,衝撃波を正弦波と仮定して計算より得られたLrとt0/Trとの関係を調べた。各減衰定数ごとの計算値と実測値を比較して図ー10に示す。図よりLrは非常に小さな値となり,実測変位を直接パラメーターとして用いれば,この影響を強く受けることがわかる。
3.3 地盤ばね定数
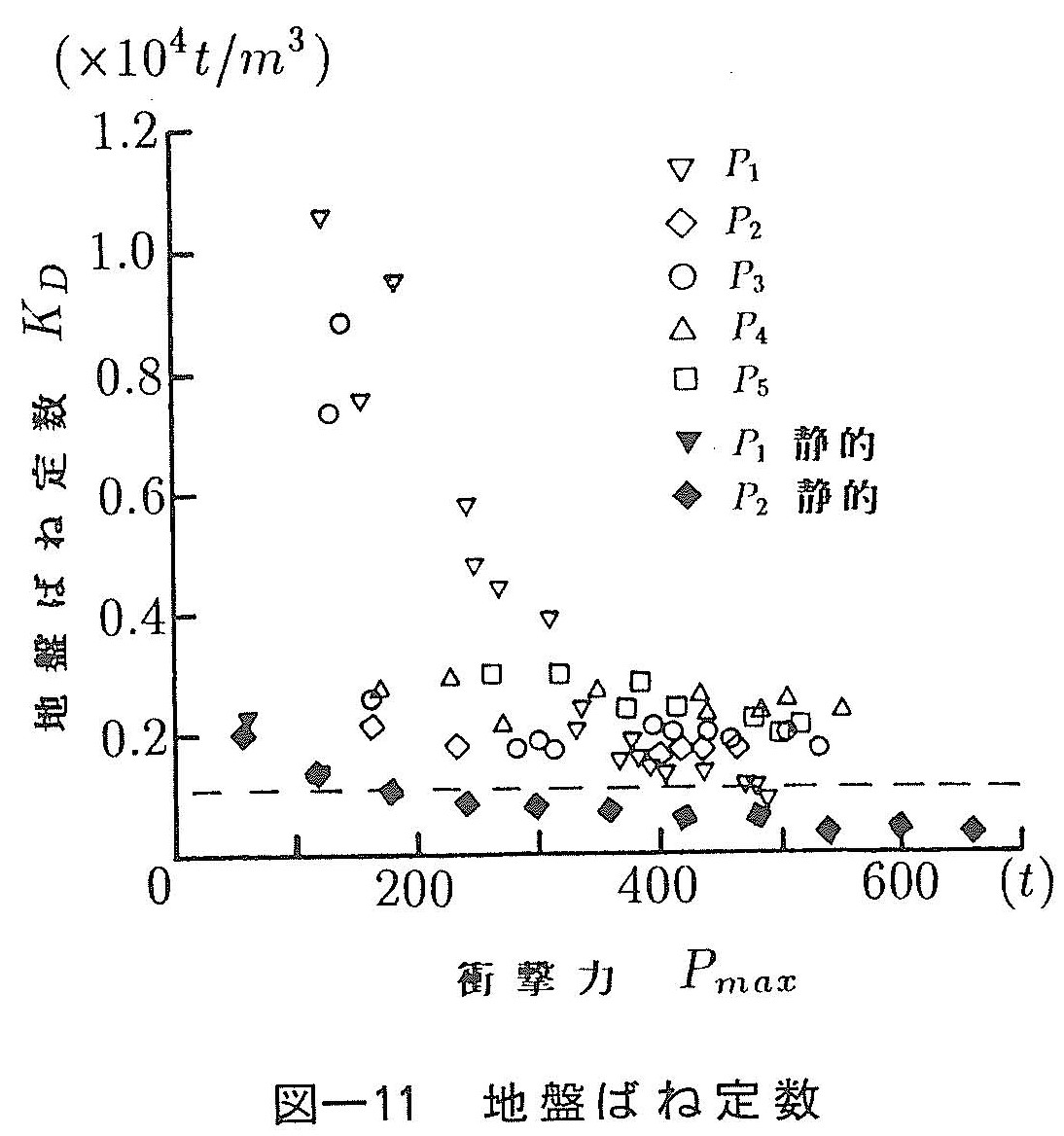
(9)式を用いて求めた動的地盤ばね定数KDを図ー11に示す。なお,静的載荷試験が行われたP1,P2杭については,静的地盤ばね定数も示している。P1杭とP3杭では衝撃荷重の増加に伴い,地盤ばね定数が低下している。これは杭周辺地盤のひずみが増大するために,地盤の非線形性が現れたものと考えられる。これに対して,P2,P4,P5杭ではKDはほぼ一定値となっており,非線形性の発現は認められない。一方,静的ばね定数Ksも載荷荷重の増加により低下するが,その傾向はKDに比べ小さい。一般に,静的ばね定数は動的ばね定数の数倍であると言われているが,図ー11についてみると,P1杭で1.8~6.2倍,P2杭で約2倍となっており,この倍率は荷重レベルで異なることがわかる。なお,図中の破線はP1,P2杭について,道路橋示方書により求めた地盤ばね定数であり,静的ばね定数Ksのほぼ平均的な値となっている。
3.4 衝撃力—静的変位曲線
各落下高さにおける衝撃力PmaxとKDが明らかとなれば,(10)式を用いてPmaxが静的に作用した場合の杭頭沈下量δstを求めることができる。
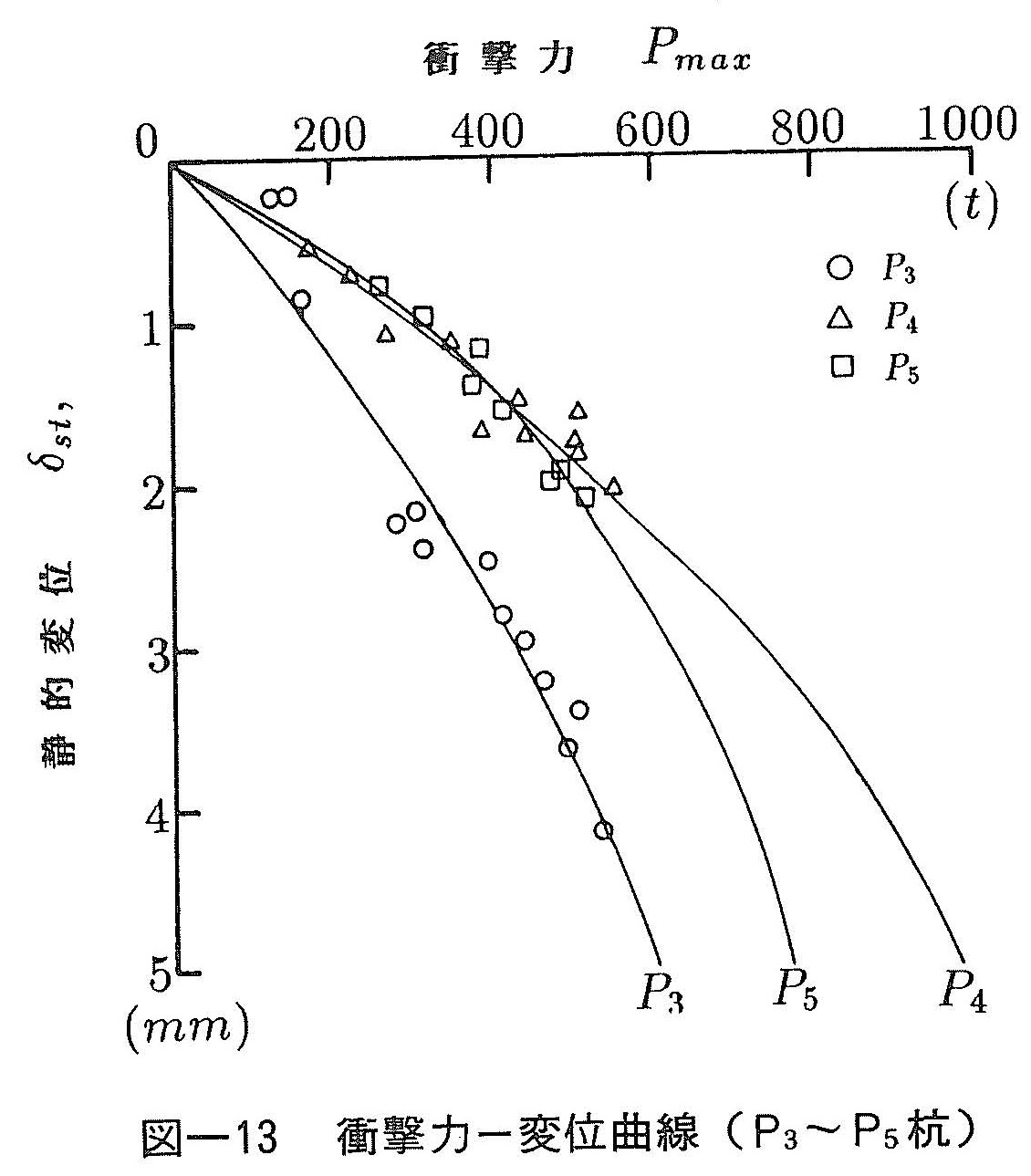
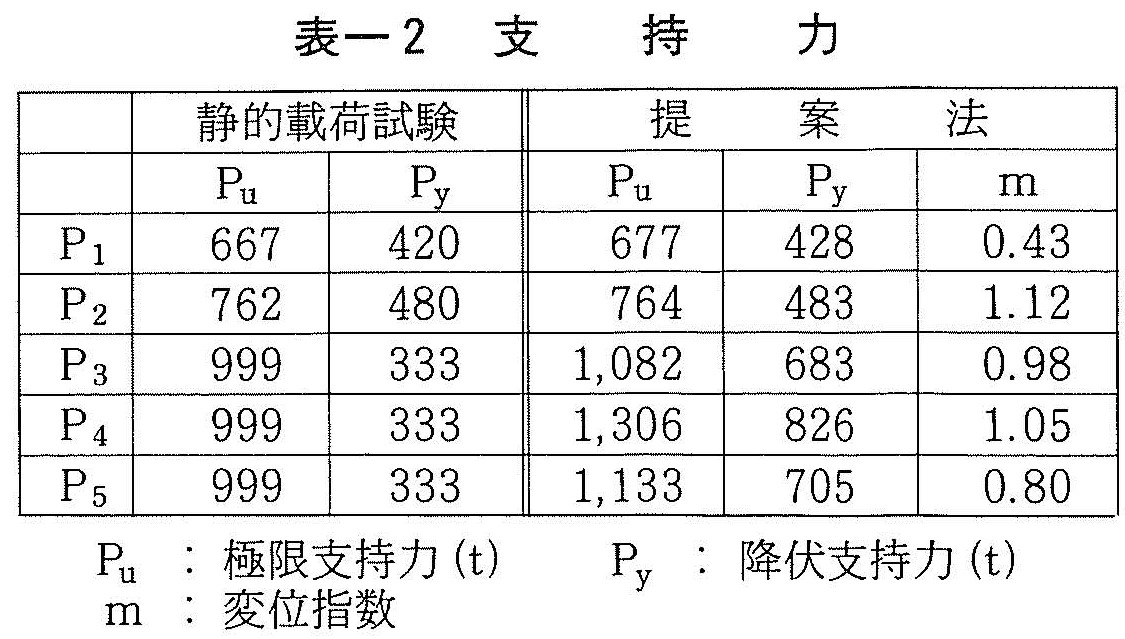
図ー12(a)(b),図ー13はPmaxーδstの関係を各杭に対して求めたものである。図ー10ではP1,P2杭の静的載荷試験より得られた荷重ー沈下関係も合わせて示している。これらの関係より得られた極限支持力を表ー2に示す。ここで,P3~P5杭については静的載荷試験が実施されなかったために,設計支持力を示している。
この表より,P1,P2杭については提案法と静的載荷試験の結果はよく一致しており,本提案法は有効であるといえる。ワイブル曲線を用いて極限支持力を精度よく推定するためには,降伏荷重以上の載荷を行い,変曲点を明白にする必要があることから,本推定法は地盤の非線形性が発現しやすい摩擦杭に対して,有効な手法であると考えられる。

4 結論
静的載荷試験に代わり,衝撃試験により場所打ち杭の支持力推定法を提案し,実杭に対する試験によりその妥当性を検討した。その結果,次のことが明らかとなった。
(1) 衝撃試験による杭の動的挙動は剛体振動と伸縮振動に分離することができ,この剛体振動では杭が排除した土の質量が付加質量となることが明らかとなった。
(2) 衝撃力の大きさで変化する剛体振動の固有円振動数と(1)の結果を用いて,地盤ばね定数の変化を求めることができる。
(3) 5本の実杭の対する試験より,杭周辺地盤の非線形性が発現しやすい摩擦杭に対して,提案推定法は有効であることが確認された。
しかし,杭はその形状や設置地盤等の影響を大きく受けるため,今後もデータの蓄積を図る必要があろう。
参考文献
1)烏野,麻生,松井,前田,場所打ち摩擦杭の支持力推定,杭の打込み性および波動理論の杭への応用に関するシンポジウム発表論文集,pp.115~118,1989
2)UNO,K.,et.al.,Bearing Capacity of Cast-in-place Piles,Proc.Of the Discussion Session 14.Drivability of Piles,12th I.C.S.M.F.E.,pp.35~38,1989
3)ASO,T.,et.al.,The Dynamic Behavior of a Cast-in-place Pile during Percussion Test, Mem.Of Fac.Of Eng.Kyushu Univ.vol.50,No.3,pp.219~238,1990
4)Smith,E.A.L.,PILE DRIVING ANALYSIS BY THE WAVE EQUATION,Proc.Of A.S.C.E.,Journal of the SOIL MECHANICS AND FOUNDATION DIVISION,pp.35~61,1960
5)Goble,G.G.et.al.,THE ANALYSIS OF PILE DRIVING A-STATE-OF-ART,Intl.Seminar on the Application of Stress-Wave Theory on Piles,pp.131~150,1980
6)日本道路協会,道路橋示方書・同解説 下部構造編,日本道路協会,1990
7)Nishida,Y.,Sekiguchi,H.and Matsumoto,T.,Stress wave monitoring for a friction pile during driving:A new analysis procedure,Soils and Foundations,JSSMFE,Vol.26,No.4,pp89~104,1986
8)Scanlan,R.H.,Tomko,J.J.,DYNAMIC PREDICTION OF PILE STATIC BEARING CAPACITY,Proc.Of A.S.C.E.,Journal of the SOIL MECHANICS AND FOUNDATION DIVISION.pp.583 604,1969
9)小坪,土木振動学,森北出版
10)塩井,宇都,冬木,近藤,桜井,杭の荷重—変位曲線の非線形回帰結果による支持力の一評価法,第23回土質工学シンポジウム発表論文集,pp.9~16,1978
11)宇都,冬木,桜井,杭の載荷試験結果の整理方法,基礎工Vol.10,NO.9,pp.21~30,1982
12)宇都,冬木,近藤,波動理論による打込み時くい頭応力の算定式について,土木学会第30回年次学術講演会講演概要集第3部,pp.163~164,1975
13)松尾,菅井,金,鋼管杭の極限支持力推定法に関する研究,土木学会論文集第406号/Ⅲ-11,pp.253~262,1989




