山岳地の多いわが国では，約20万ヶ所にも及ぶ斜面崩壊危険箇所が指定されており，毎年降雨，地震といった誘因によって土砂災害が多発し，人命や財産の損失は大きな社会問題となっている。斜面崩壊は避けることのできない自然現象であり，その発生そのものを防止することは困難であるという認識から，大災害とならないように崩壊の発生を適確に予知して，それに基づく防災対策が求められている。

崩壊発生の予知を行うには，まず対象となる斜面の力学的平衡に基づく安定解析を行うことが最も信頼性のある基本評価技術であり，これまで多くの解析法が提案・開発されてきた。しかしながら，これらの解析法は盛土，切土などの，あらかじめ決められた斜面が対象である。崩壊の予知には，更に「いつ（時期）」「どこで（位置）」および「どの程度（規模）」の3つを知ることが求められる。これらが地形，地質などの調査データ，降雨などの計測データから精度よく求められると自然災害の軽減や供用中の斜面の維持管理に役立ち，安全，安心の社会の実現に寄与できると考えられる。われわれの研究グループは，広域の斜面（同一の地質構造からなる管理区域，危険指定地など）の中から，これらの3つの予知を可能とする技術の確立のために，三次元斜面安定解析を基本解析ツールに据えて，斜面崩壊に関連する様々なデータを最新のGIS技術を用いて時間的，空間的に処理して，崩壊のメカニズム・過程を忠実に反映した斜面崩壊予知システムの実現を目指している。

今回は1990年から1996年の雲仙普賢岳噴火活動によって形成された溶岩ドームの斜面安定評価を試みる。

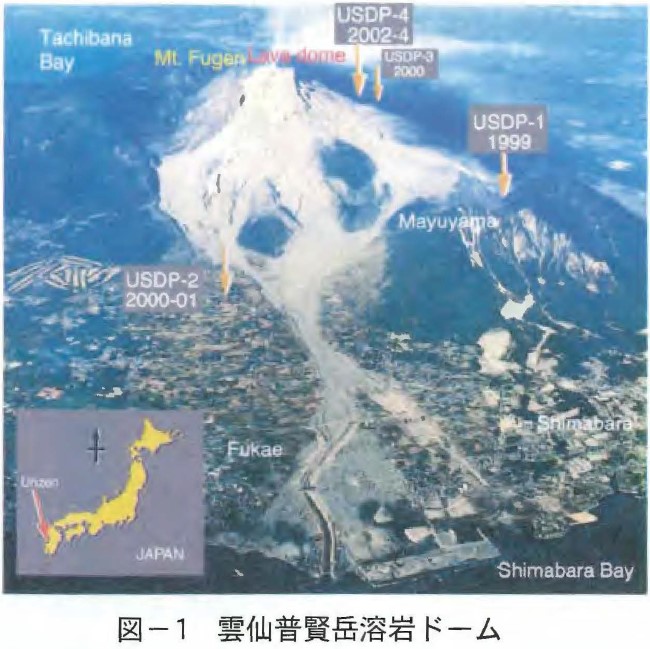
長崎県島原半島の中央に位置する雲仙普賢岳（標高1,359m)は，1990年11月17日，198年ぶりに噴火活動を開始した。翌年5月20日に最初の溶岩ドームが出現し，4日後から溶岩ドームの崩落により初めての火砕流が継続して，死者・行方不明者43人，被害総額2,300億円に達する長期にわたる甚大な被害を生じた。また，火山灰や火砕流が堆積した山地斜面は，時間雨量十数mmの降雨で頻繁に土石流を発生させた。1995年5月25日，火山活動の停止宣言が発表され，溶岩ドームの成長が停止した。しかし，その後も小規模の崩落は継続している。1792年の「島原大変，肥後迷惑」で知られる眉山崩壊は，眉山自体が過去の火山活動による溶岩ドーム状の山体であり，約1億5000万立米という巨大崩壊と推定されている。平成新山（標高1,486m)を形成する溶岩ドームは約1億立方米程度，その直下の谷を埋めた斜面は傾斜約35゜である。現在の溶岩ドームは安定なのか，また崩壊するとすればどのような規模で生じるのか不明であり，ドームの安定性評価が求められている（図ー１)。

従来の斜面安定評価手法を総括してみると，力学的解析法と数学・統計的解析法（多変量解析，数量化理論，遺伝的アルゴリズム等）に分けられる。力学的解析法は，数学・統計解析法と比べ，斜面そのものの力学的安定性を定量的かつ客観的に評価できるので，多くの研究がなされ，技術的に成熟しているといえよう。現在では汎用ソフトが市販されて，最もすべる可能性のあるすべり面の形状と安全率を計算できる。しかし，基本的には切土や盛土を対象とするもので，そのほとんどは垂直二次元断面での取扱いである。また，実際に生じる崩壊は三次元の形状を有することから，三次元解析が理想と考えられるので三次元斜面安定解析法も提案されている^2)-6)。しかしながら，極めて煩雑なメッシュ分割や幾何データの整理が現実的に困難なことから，一様な傾斜を有する斜面問題に限られており，複雑な自然地形の中から崩壊の形状を抽出するには至っていない。また，これらの力学的解析法を自然斜面の安定性評価に適用するには客観的に崩壊位置を推定する手段が求められる。

他方，降雨と斜面崩壊の関係については，多変量解析などによって，降雨と崩壊・未崩壊の判断を求める研究が行われている。時間最大雨量，降雨強度などの短期雨量指標および先行雨量，累積雨量や実効雨量などの長期雨量指標との両者の関係を用い，実際に崩壊を引き起こしたデータに基づき崩壊予測や警戒・避難基準雨量を求めている⁷⁾。しかし，これらは経験的知見に基づくもので，斜面崩壊のメカニズムを含んでいない。また，降雨観測域内での地域単位であるため，区域内のどの位置で崩壊が発生するか特定することができない上，空振り率が高いなどの多くの問題が残されている。以上の状況を踏まえ，著者らは，広域の自然斜面の中から不安定な斜面の「位置」と崩壊が想定されるすべり体の「規模」を求めるための三次元斜面安定解析の開発研究を行ってきた^8)-10)。

次に崩壊時期の予測について考えてみる。一般に斜面は，地震を除けば，降雨にともなって崩壊を生じるケースがほとんどである。すなわち地質的侵食輪廻の過程にある，崩壊が迫った比較的安全率の低下している斜面が，降雨が引金となって崩壊すると考えると，時々刻々の降雨のデータをもとに，地下浸透，地下間隙水圧の上昇，斜面の不安定という力学過程を明確にすれば「発生時期」が得られることになる。現在ではアメダス降雨データが全国もれなく1時間毎に遅延なく得られるし，最新のレーザ雨量観測データは１㎢面毎に雨量を取得できるが，残念なことに未だ斜面安定解析とは結び付けられていない。

われわれは，土砂災害予知に真に役立つための，広域にわたる複雑な地形・地質からなる自然斜面の三次元的安定性を定量的に評価する技術の確立を最終目標としている。すなわち，不安定なすべり体を客観的に抽出して，その位置，規模に加えて時期も予測できるシステムをめざした以下の取り組みを行っている。

斜面安定解析には，対象区域内の地表標高，地層，地下水位などのデジタルデータが必要である。従来の紙地図をベースとした作業方法では，このようなデータの作成作業は極めて困難である。そこで，GISを導入することによって，標高のラスターデータを得る。最近整備が進んでいる航空機レーザ測量データの場合はそのまま使用できる。標高のラスターデータをベースに，空間解析により各セルでの傾斜角度，傾斜方向の分布を計算する。地層や地下水面の分布も同じプロセスでデジタル化する。

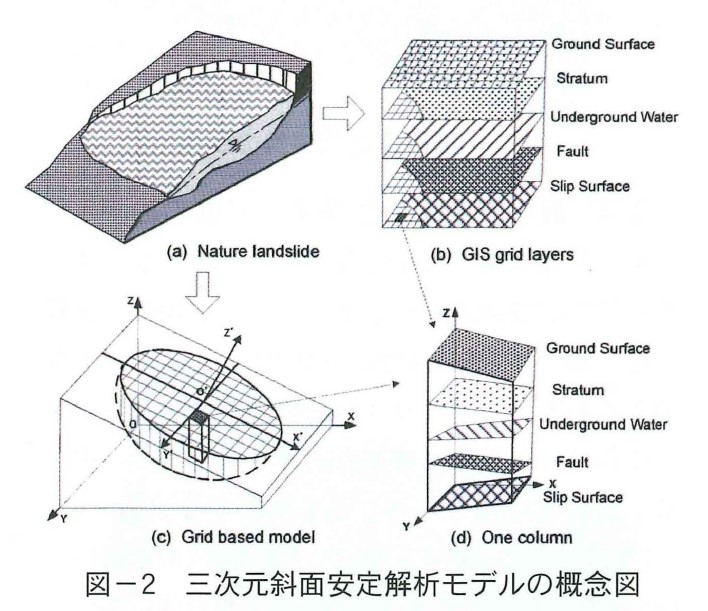
図ー２のように，まず，地形，地層，地下水位などの空間情報をGISラスターデータに変換し，各ラスターレイヤーを作成する。次に，すべり体範囲内の各セルに対して，それぞれのラスターレイヤーが持つ空間情報を下式に代入し，すべり方向に作用する各セルのすべり力と抵抗力を計算する。さらに，すべてのセルのすべり力と抵抗力をそれぞれ合計し，その比を三次元すべり安全率として求める。

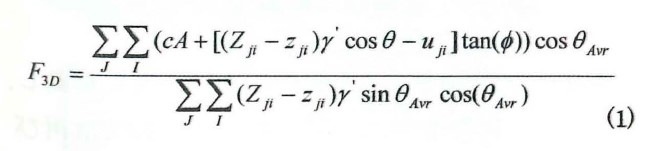
ここに，i,jはすべり体範囲内のセルの行と列数，cはすべり面の粘着力，Φは内部摩擦角，Aは各土柱のすべり面の面積，θは各土柱のすべり面の傾斜角度，θ_Avrはすべり体の主傾斜角度，Z_jiは(i,j)番目の各土柱の表面と底面の標高，μ_jiは(i,j)番目の柱状体底面に作用する間隙水圧，γ’は柱状体の単位重量である。式(1)はHovlandの式（著者が一部修正）であるが，Janbu,Bishopの三次元拡張式の導入も可能である¹²⁾。

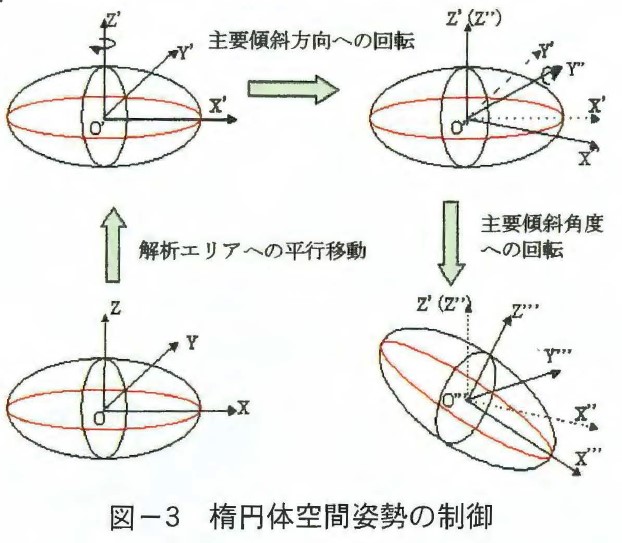
三次元で斜面安定性を評価するために，すべり体の空間形状を特定する必要がある。過去多くの斜面崩壊事例から，すべり面の三次元形状は楕円体の下半部分に相当するケースが多いので，すべり体の空間形状を楕円体と仮定する。その際，楕円体の空間姿勢を決める必要がある。楕円体の空間姿勢と寸法は，中心点位置，傾斜方向，傾斜角，および楕円体の径a，b，cによって決定される。次に楕円体の径a，b，cすなわちすべり体の長さ，幅，深さをパラメータ変数として可能性のある最大値と最小値を指定する。更に楕円体の中心位置と空間姿勢を任意に制御できるようにする。空間姿勢はその斜面の傾斜方向に座標変換を行なう(図ー３)。次に楕円体の中心位置，および寸法を変化させることによって，様々な潜在的なすべり面の形状を作り出す。このすべり面で囲まれた想定される全てのすべり体に対して，三次元安定計算を行う。

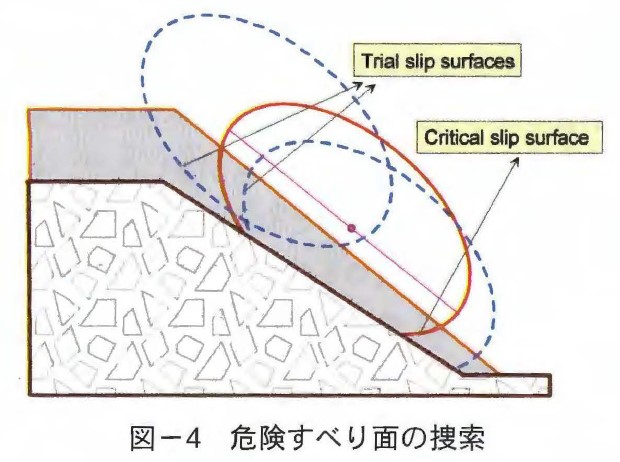
すべり安全率が最小となるすべり体を抽出するために空間捜索計算が必要である。空間捜索計算の際楕円体の中心位置，楕円体の寸法を可能性のある範囲でモンテカルロ法により一様乱数として任意に設定し，多くの試行計算を行う。その中で、最小安全率を持つすべり面を抽出する（図ー４)。

COM(Component Object Model)技術を用い，GIS機能を実現するコンポーネント集合体によって，以上の計算過程を統合した総合的な斜面安定解析システムを開発した。

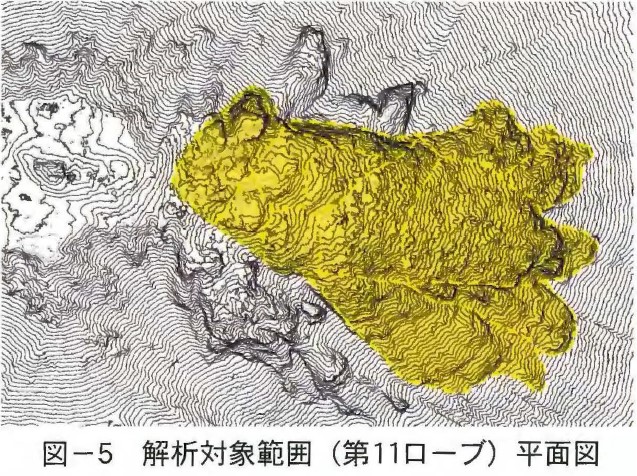
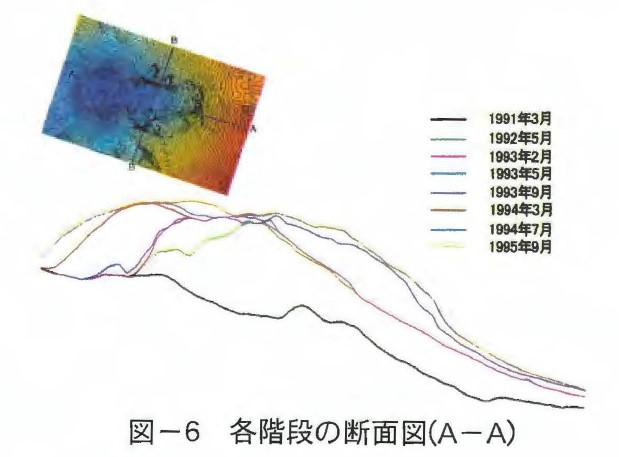
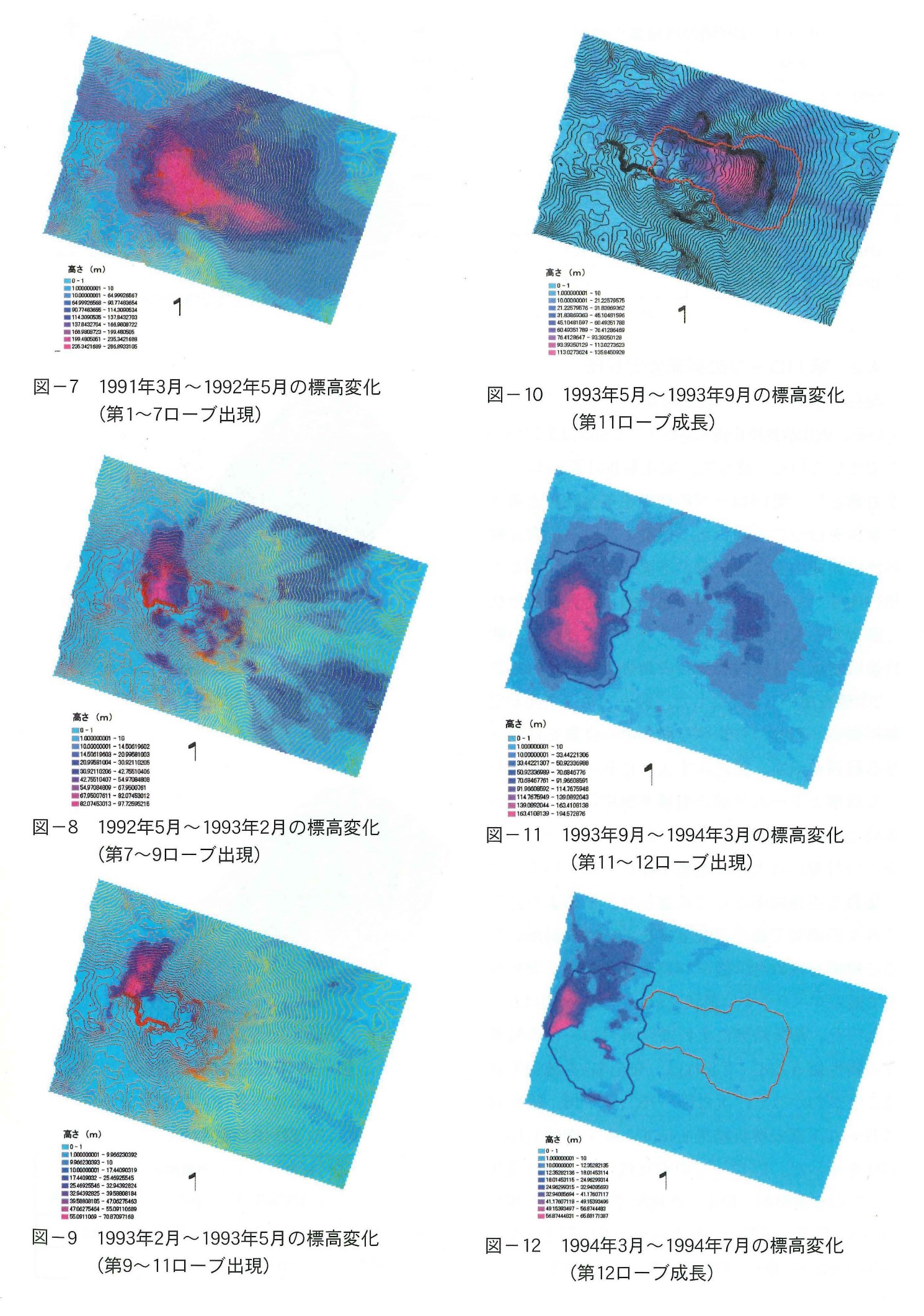
溶岩ドームは火山活動の中で次々に形成され，現在では図ー５に示すように第11ローブがほぼ全体を覆っている。現在この変遷の記録として残存するのは，この平面図のスケッチと空中写真のみである。空中写真は本格的な活動が始まる前の1991年3月から活動が終息した1995年9月までの間に8回撮影されている。この空中写真から土地標高数値データ(DEM)を作製し，GISを用いて8回のデータを重ね合せた。図ー６に第11ローブの中央での各段階の断面を示す。また，図ー７～図ー12に各段階での標高の変化状況を示す。これによれば図ー７に示す1992年5月までの1年間は最も活動期であり，第7ローブまで出現した。この間の体積増加は1億立米を超え，ドーム中央部は標高1,480mまで盛り上り，下部の谷は100～200mの堆積物で埋尽された。図ー７の中央の赤い部分は約200m隆起しているが，その周辺も高くなっている。この変化は山体の膨張と表面のローブの堆積によるものであるが，大半は山体の膨張であり，ローブはその表面を薄く覆っているものと考えられる。

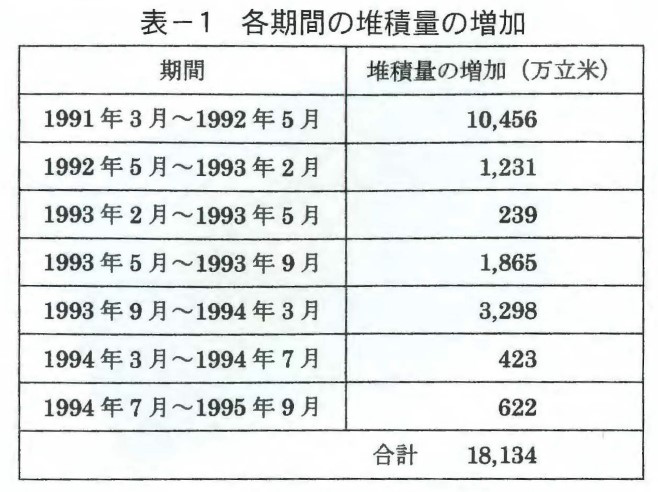
次の図ー８，図ー９では，火山活動は西部に移動し，図ー10では再び中央部，図ー11，図ー12では再び西部へと降起部が移動した。これらの変遷と体積の変化を表ー１に示す。ドーム下方の堆積物も含めた溶岩ドームの体積は約1.8億立米である。

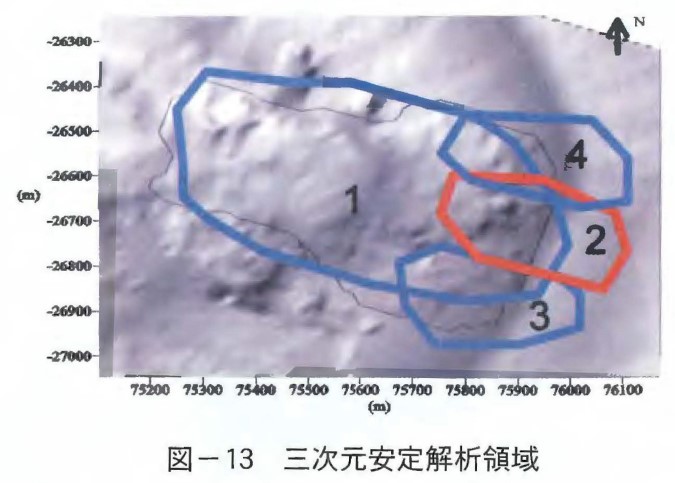
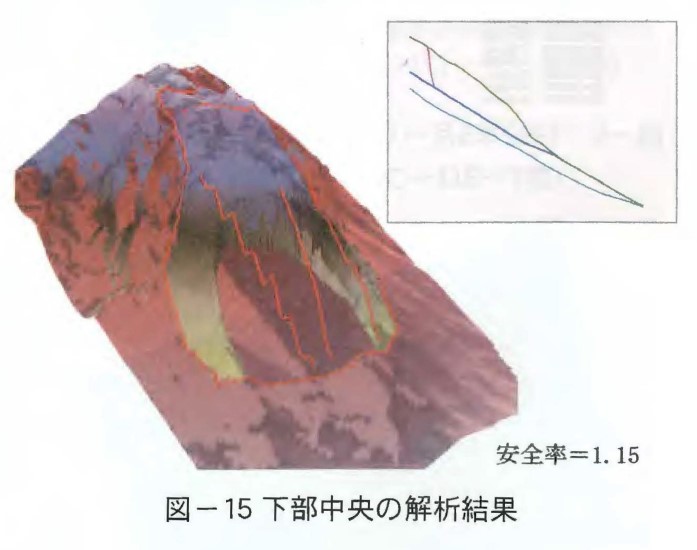
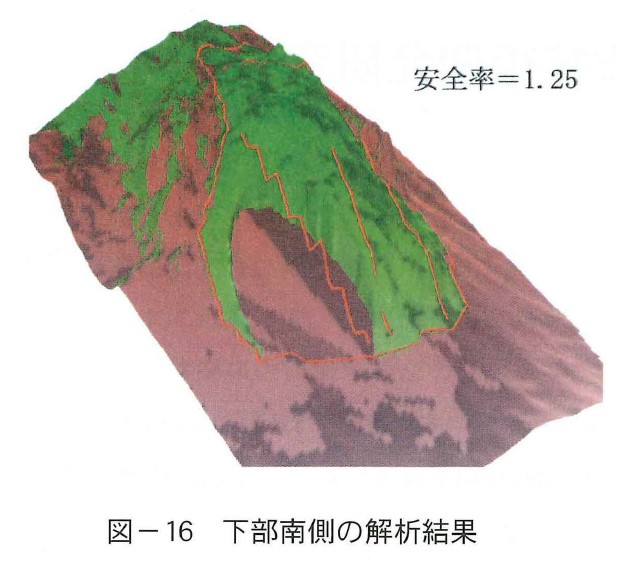
現在の溶岩ドームの表面は第11ローブで覆われている。火山活動停止後も時折生じる崩落は第11ローブで生じている。従って，安定解析は第11ローブを対象とし，第11ローブの底面を不連続面と考えて解析を行うことにした。提案している三次元解析法は斜面内部に流れ盤の不連続面が存在すると，楕円体すべり面の一部が不連続面で切られた形状で解析することができる。入カデータとしての物性値は観測手法検討委員会の調査で求められた表ー２の値を用いることにした。図ー13に三次元安定解析領域，すなわちすべり面の中心位置を移動させる範囲を示す。図に示すようにドーム全体にわたる崩壊とドーム下部の崩壊を想定して，4つの領域に分けて解析を行った。また，11ローブの表面には目視から大きな亀裂が認められている。この亀裂を不連続面として考慮した。このようにして各々の領域で最小の安全率をとる崩壊斜面の位置と規模を求めた。図ー14に全体にわたる安定解析で最もすべりやすい形状を示した。安全率は1.37となった。解析結果によれば第11ローブの境界面の物性値Φ〉28゜であれば，安全率1を確保できることがわかった。次に図ー15，図ー16，図ー17にドーム下部の解析結果を示す。安全率は1.15～1.31を示した。11ローブの安定性については全体としての安全率が，仮定した地盤定数を用いた場合，1.3～1.4程度，下部はそれよりやや低い程度となり，下部の方が相対的に崩壊しやすいと考えられる。

末尾ながら，本解析は，平成15，16年度に行われた「雲仙普賢岳溶岩ドーム観測手法検討委員会」の中で実施されたものである。委員各位，雲仙砂防事務所，および（財）砂防地すべりセンターの皆様には多大なる御指導と御援助を賜わりました。厚く御礼申し上げます。

参考文献