我が国では，戦後の急速な経済成長に伴ってこれまでに多くのコンクリート構造物が造られてきたが，これらの中にはアルカリ骨材反応や塩害，重交通量の急激な増加，乱雑な施工等に基づく各種の欠陥を有するものもかなり含まれていることが明らかになり，コンクリート構造物の早期劣化が大きな社会問題となっている。そこで，これらの構造物の安全性確保と有効利用の見地から，コンクリート構造物の各種欠陥を早期に発見し，適当な処置を施して構造物の供用期間をできるだけ永く保つため欠陥評価法の確立が急務となっている。筆者は以前より，発信器のスィープモード入力に対する受信波の応答スペクトルを利用して，部材および構造物中の各種欠陥（ひびわれ，空隙，劣化度等）を非破壊的に評価する方法について検討している。ここでは，本方法によるコンクリート部材および構造物中の各種欠陥評価の可能性について検討した結果を述べる。

一般に，材料中を伝播する超音波の周波数特性を得る方法として，パルス入力に対する受信波のフーリェ解析が行われている。これに対して，発信器のスィープモード入力（振幅一定で漸次その周波数が変化するSine波形の連続波）に対する受信波の時間一振幅曲線（すなわち応答スペクトル）を利用する方法が考えられる。フーリェ変換による方法が，瞬時の時間波形を精度良く記録し，出来るだけ短い時間で周波数成分を取り出すために，高速度，大容量のデジタルメモリーと波形解析器またはコンピュータを必要とするのに比べて，この方法では簡単な計測器のみでシステム化が可能であるので，現場計測等に手軽で便利であり，また経済的であると考えられる。

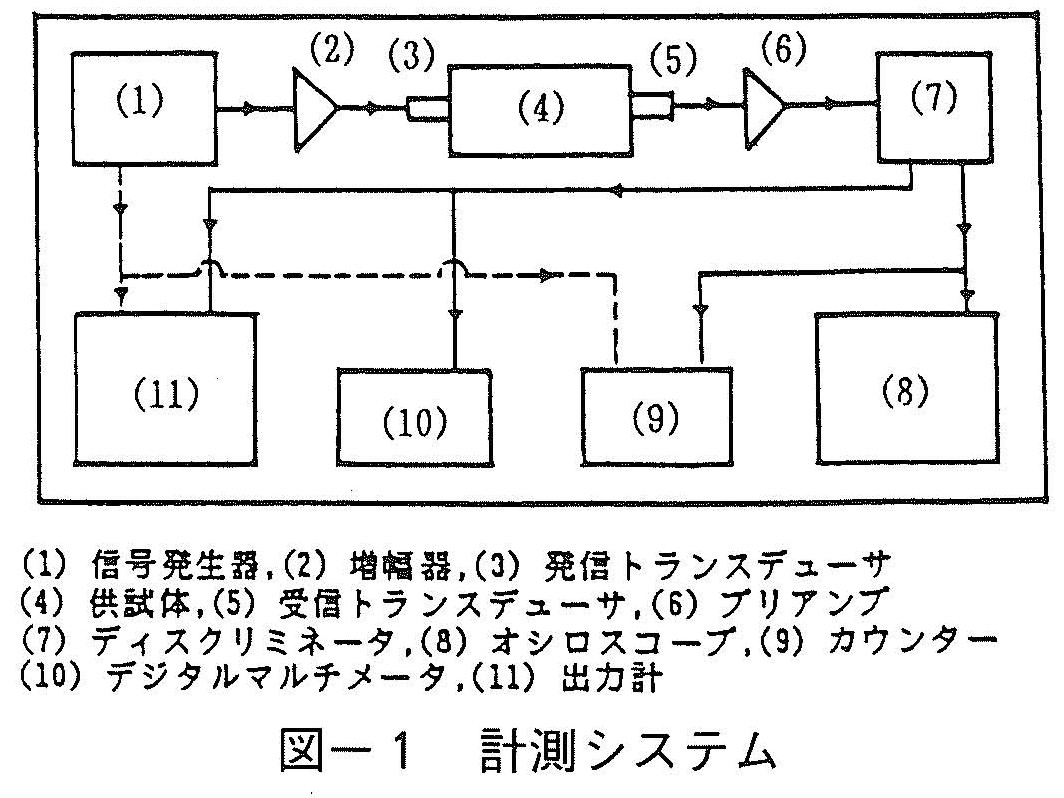
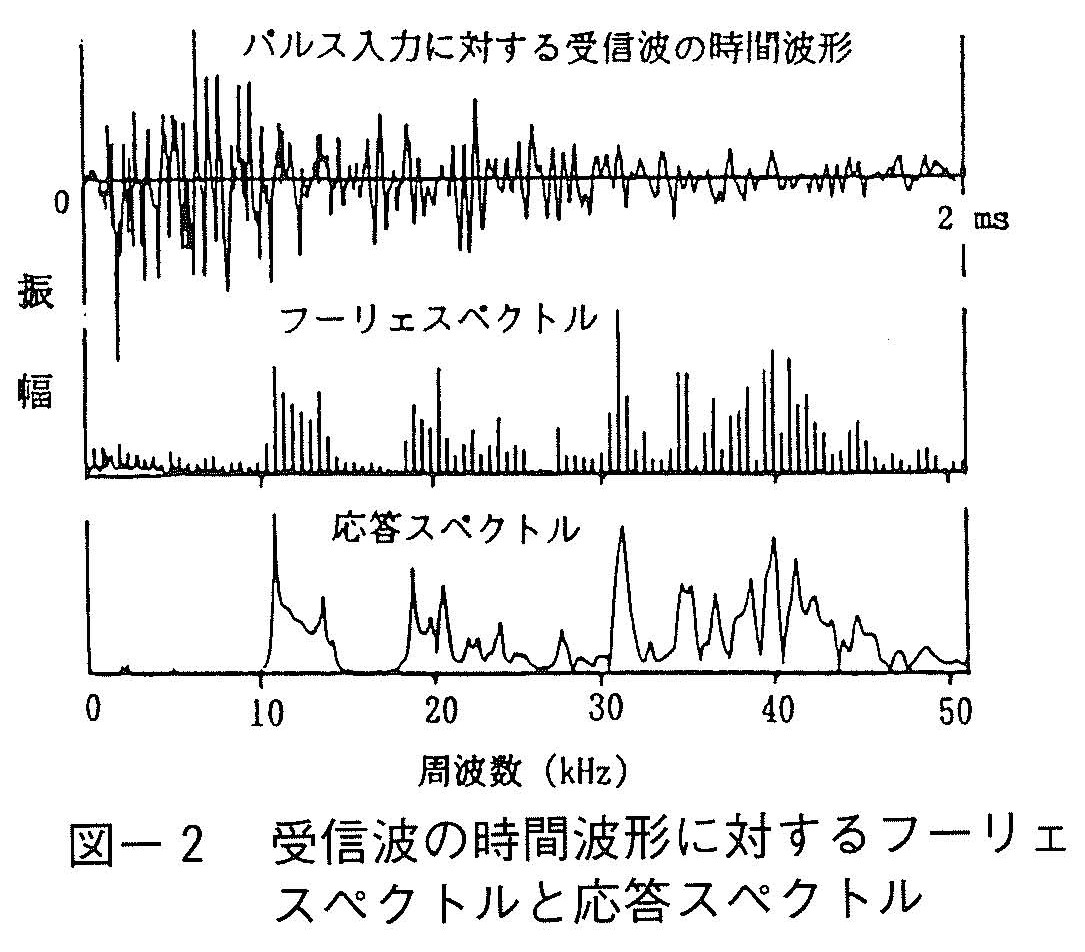
図－１は本方法における計測システムを示している。発信器を出た電気信号は増幅器を経て発信トランスデューサにて応力波に変換されて供試体に入射し，供試体中を伝播して供試体の他端に取り付けられた受信トランスデューサに感知される。そこで，応力波は再び電気信号に変換され，プリアンプ，ディスクリミネータで増幅，検波されてオシロスコープや記録計，出力計にて観測，記録される。本方法によって得られる応答スペクトルは本質的にフーリェスペクトルに等価であり^1），図－２はその等価性を示す一例を示している。この図は，角柱供試体（10×7.5×40cm）に発信および受信センサを固定したまま得られたフーリェスペクトルと応答スペクトルを示している。フーリェ解析では有限個のデジタルデータを高速フーリェ変換（ＦＦＴ）して，ある周波数間隔でその成分を取り出すため，断続的に周波数成分が並べられていて尖鋭な感じもするが，そのエンベロープを考慮したスペクトルの概形は応答スペクトルにほとんど類似しており，両者は等価であることが判る。

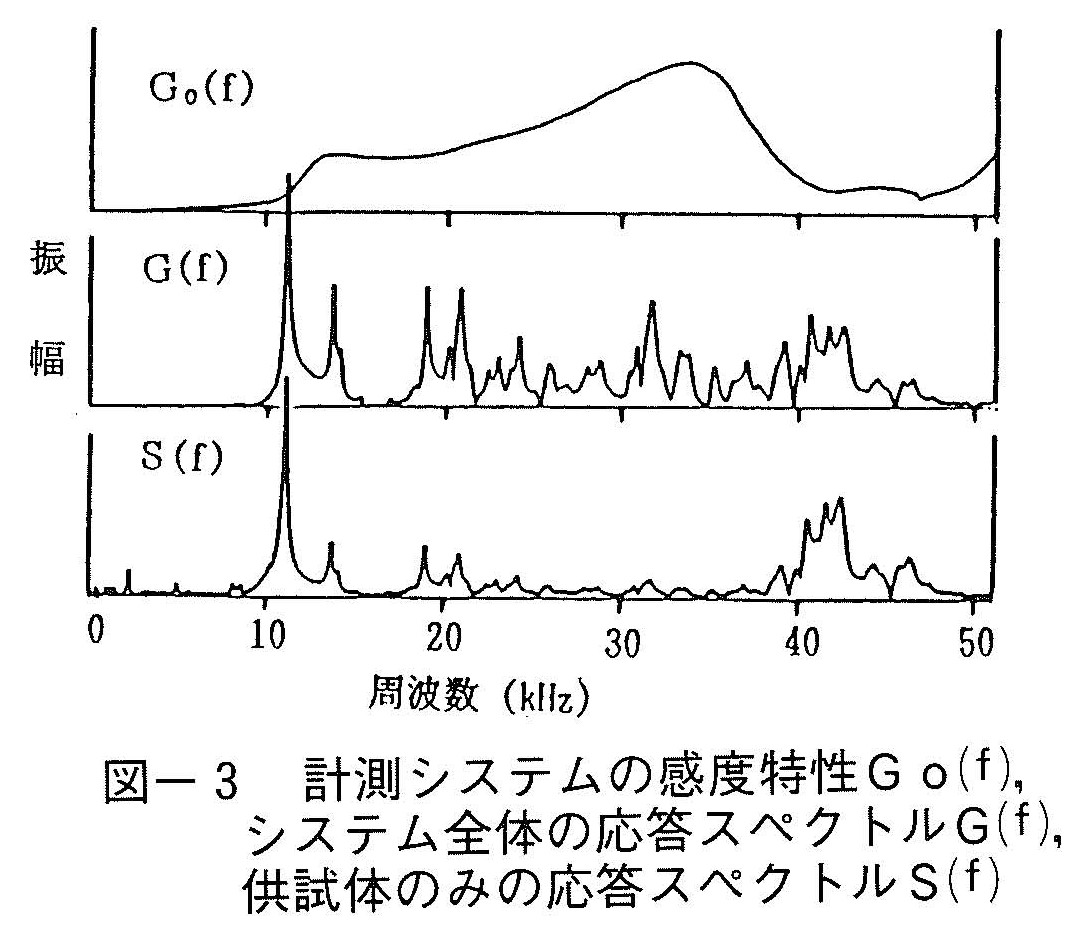
一方，計測システムにはそれ自体の周波数応答すなわち感度特性があるので，直接的に得られた応答スペクトルには被検体の周波数応答と計測機器自体の感度特性の両方が含まれている。そこで，被検体のみの応答スペクトルを得るには，直接的に得られた応答スペクトルを計測システムの感度特性で補正する必要がある。ところが，ここで使用している計測システムの感度特性は被検体の応答スペクトルに比べて非常に滑らかであるので，特に応答振幅に固執しない限りにおいて，これを補正しなくても被検体の特徴を把握できることが判っている。図－３は10×7.5×40cmの角柱供試体より直接的に得られた応答スペクトルG(ｆ)と，発信および受信センサを接触して得られた計測システムの感度特性Go(ｆ)，および補正後の応答スペクトルＳ(ｆ)を示している。滑らかなGo(ｆ)に比べてＳ(ｆ)は凹凸が激しいので，結果的に補正前後の両応答スペクトルの特徴はほとんど大差ないことが判る。それ故，以後の実験結果については全てG(ｆ)を用いて議論し，また応答スペクトルの振幅は相対的なものとしてその振幅のスケールは示さない。なお，応答スペクトルの再現性をよくする方法やスイーブ時間が応答スペクトルに及ぼす影響等，応答スペクトル測定上の留意点の詳細については文献〔１〕を参照されたい。

本方法は，材料中を伝播する超音波または弾性波の周波数特性を追求する見地から，共振法と類似点が多い。図－４はφ15×30cmの普通コンクリート標準供試体を使用して，共振法縦振動法による共振周波数と本方法による応答スペクトルを比較したものである。共振法では強弱に関係なく共振周波数を拾い出したため若干ばらつきが見られるが，矢印で示す応答スペクトル上の初期ピーク周波数と共振法の共振周波数がほぼ一致していることが判る。この応答スペクトル上の初期ピーク周波数と一致する共振周波数は，縦振動一次共振周波数であることが確認されている。これより，共振法と同様に，本方法を用いてコンクリートの動弾性係数や劣化度等，材料的性質の評価が可能であることが判る。

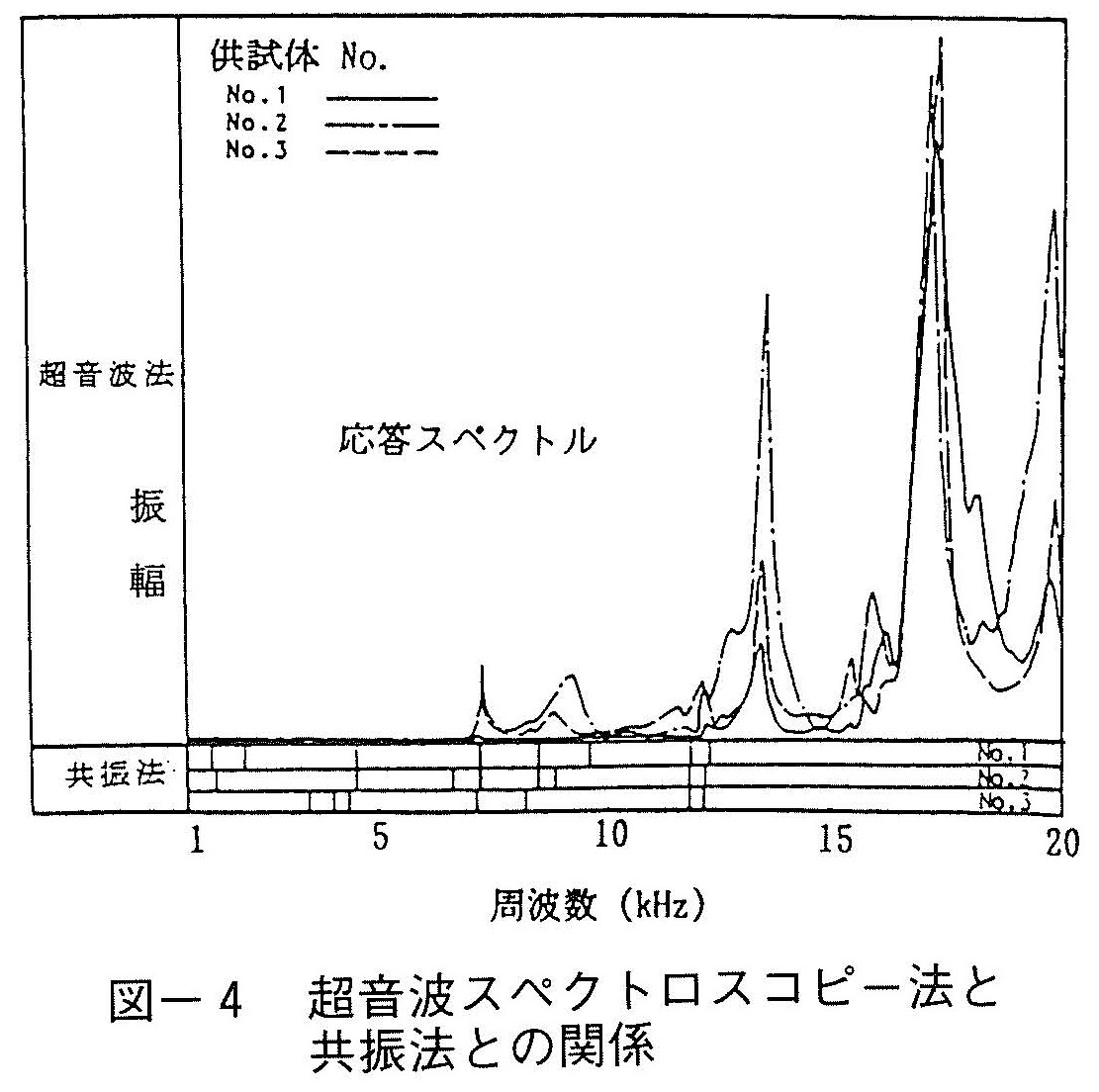
図－５は，水セメント比Ｗ／Ｃ＝55％の普通およびＡＥコンクリート角柱供試体（10×7.5×40cm）の凍結融解過程における１～10kHz間の応答スペクトルを示している。図中に矢印で示すように，普通コンクリートでは試験前において約5kHz付近にある初期ピークが凍結融解サイクル数の増加に伴って漸次低周波数側へ移動するのに比べて，ＡＥコンクリートではほとんど変化ないのが判る。このように，共振点を視覚的に捕らえられるのも本方法の特徴の一つである。

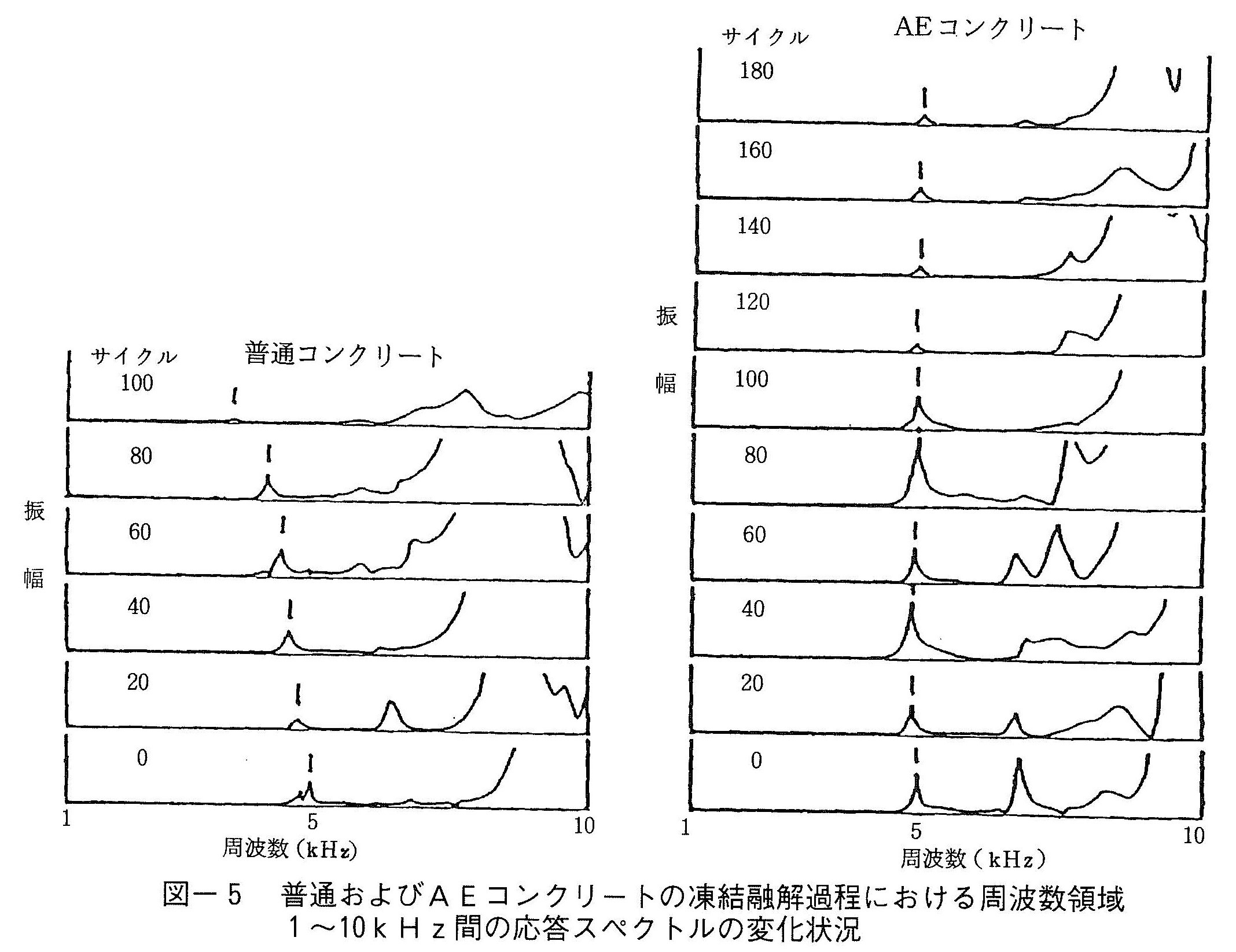
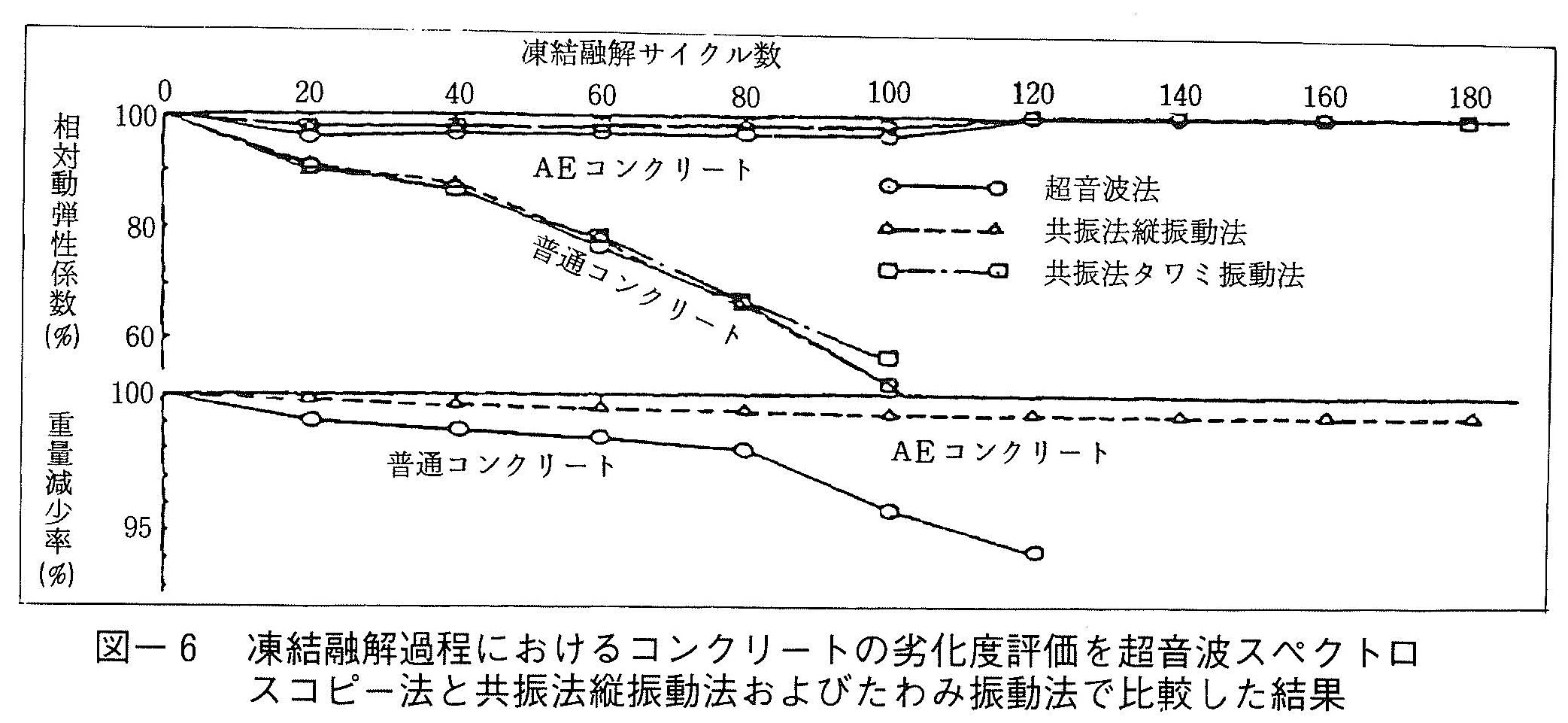
図－６は，上述の凍結融解試験におけるコンクリートの劣化過程を本方法と共振法縦振動法およびたわみ振動法の３方法で比較評価した結果を示している。本方法では初期ピーク周波数を基に，また共振法では一次共振周波数を基に，それぞれ凍結融解サイクル数の増加に伴う相対動弾性係数の変化状況を示している。３方法共にほぼ同様の結果を示しており，ＡＥコンクリートに比べて普通コンクリートの方が早く劣化し，また重量減少率もコンクリートの劣化度に伴って減少している様子が判る。

本方法では，コンクリートの材料的性質の他に，応答スペクトル上のピーク周波数を利用して，部材中のひびわれ深さ評価が可能であると考えられる。この場合，コンクリートの配合条件や供試体形状寸法が応答スペクトルに及ぼす影響について把握しておく必要がある。そこで，表ー１のような配合条件の基で，同一形状寸法の角柱供試体による部材中のひびわれ深さ評価の実験を行った。

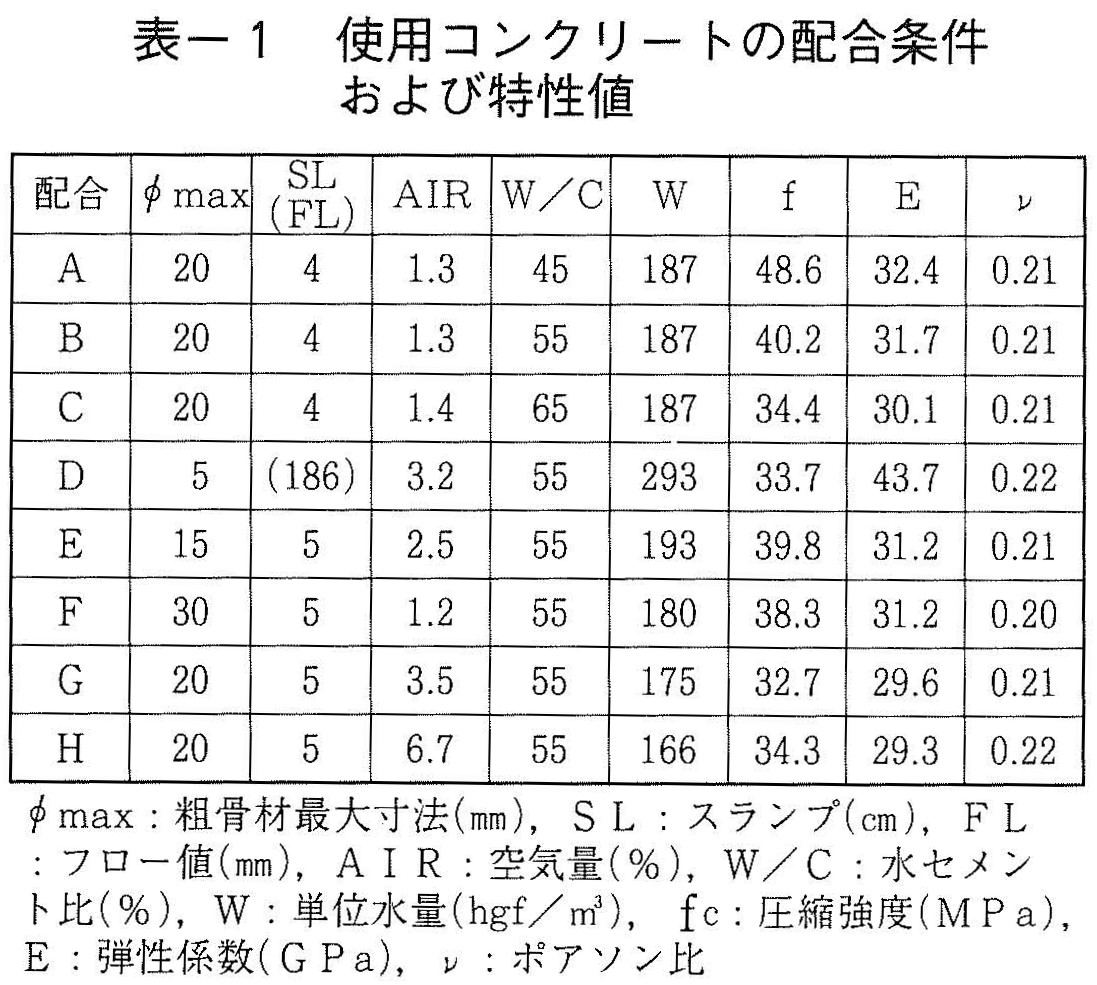
図－７はここで使用した人工ひびわれを有するコンクリート角柱供試体の形状寸法およびセンサ取り付け状況を示している。なお，人工ひびわれは幅約1.2mmのカッターにて切り欠いて導入した。

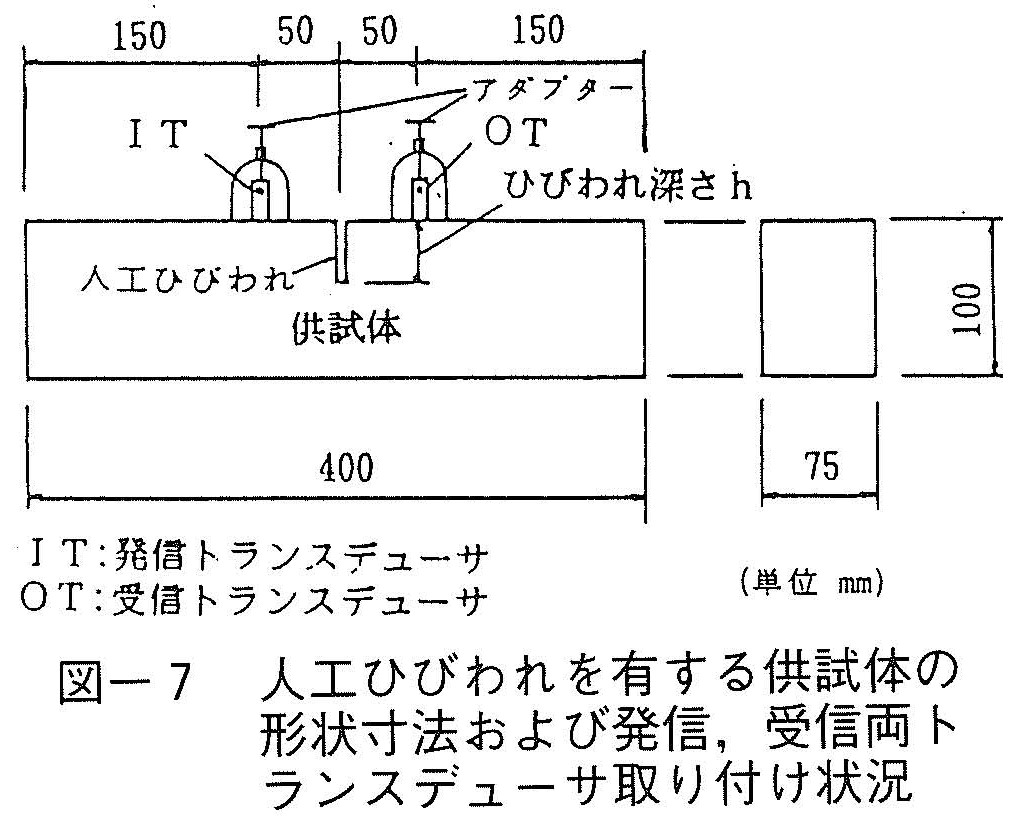
図－８は，水セメント比Ｗ／Ｃ＝45％の場合のひびわれ深さの増加に伴う周波数領域０～30kHz間の応答スペクトルの変化状況を示している。図中に矢印で示すピークＡ，Ｂ，Ｃはここで着目したピークである。ピークＡとＢは無ひびわれ部材において約12kHzと14kHz付近にあり，ひびわれ深さの増加に伴って次第に低周波数側へ移動するのに比べて，ピークＣはひびわれ深さに関係なく，終始18kHz付近に留まっている様子が判る。Ｗ／Ｃが異なる場合でもほぼ同様の傾向を示し，Ｗ／Ｃが大きくなるに従ってピーク周波数が相対的に低周波数側へ移動することが判った。これはＷ／Ｃが大きくなるほどコンクリート中の超音波伝播速度が小さくなるためと考えられる。また表ー１に示す他の配合のケースにおいてもほぼ同様のピークが存在していることが判った。これは，これらのピークが水セメント比や粗骨材最大寸法，空気量など，配合条件の相違に基づいているものではないことを示している。なお，このひびわれ深さの増加に伴う応答スペクトル上のピーク周波数の変化状況については，境界要素法（ＢＥＭ）による２次元共振解析によって理論的に確認されている。^6）

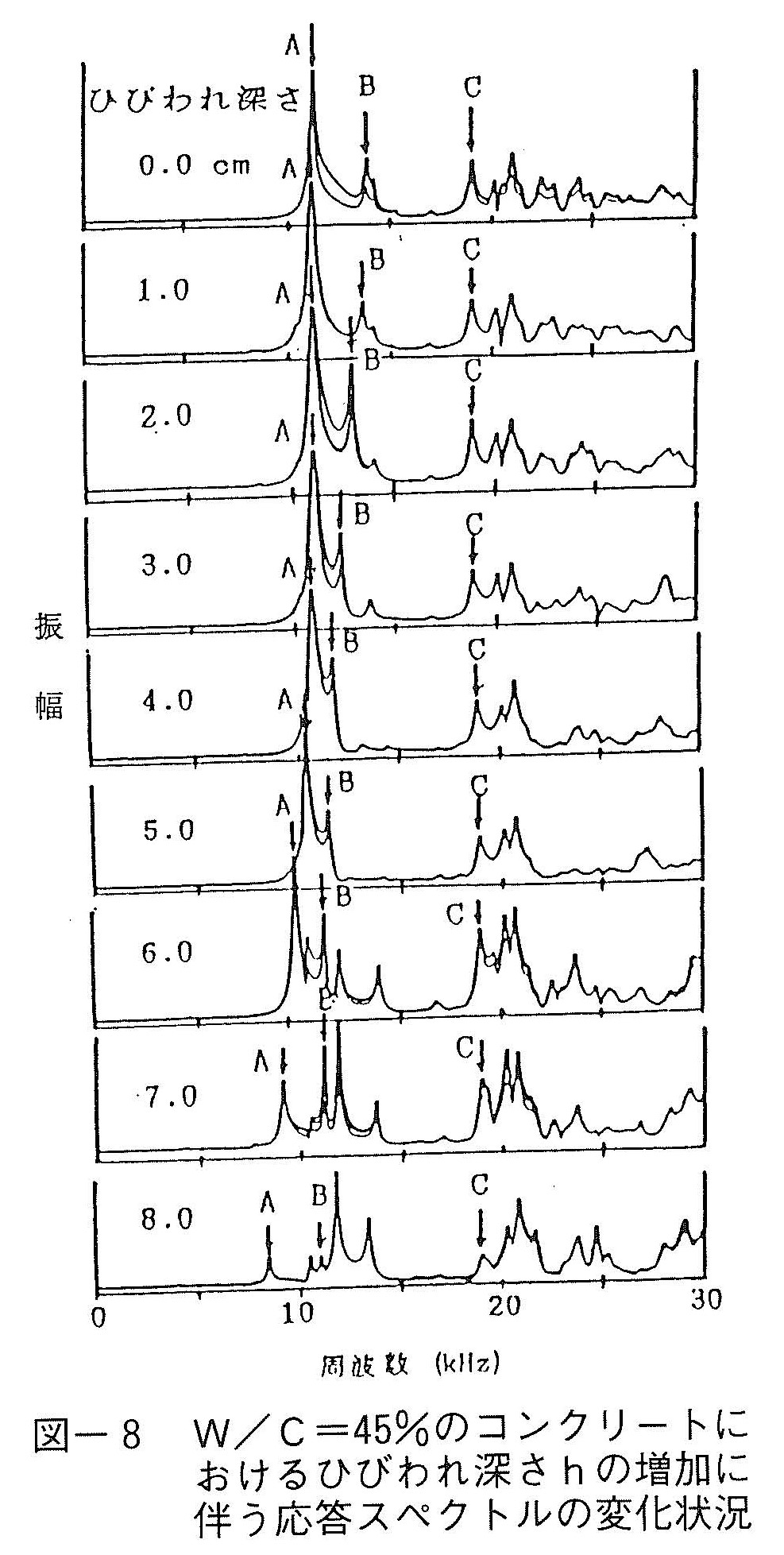
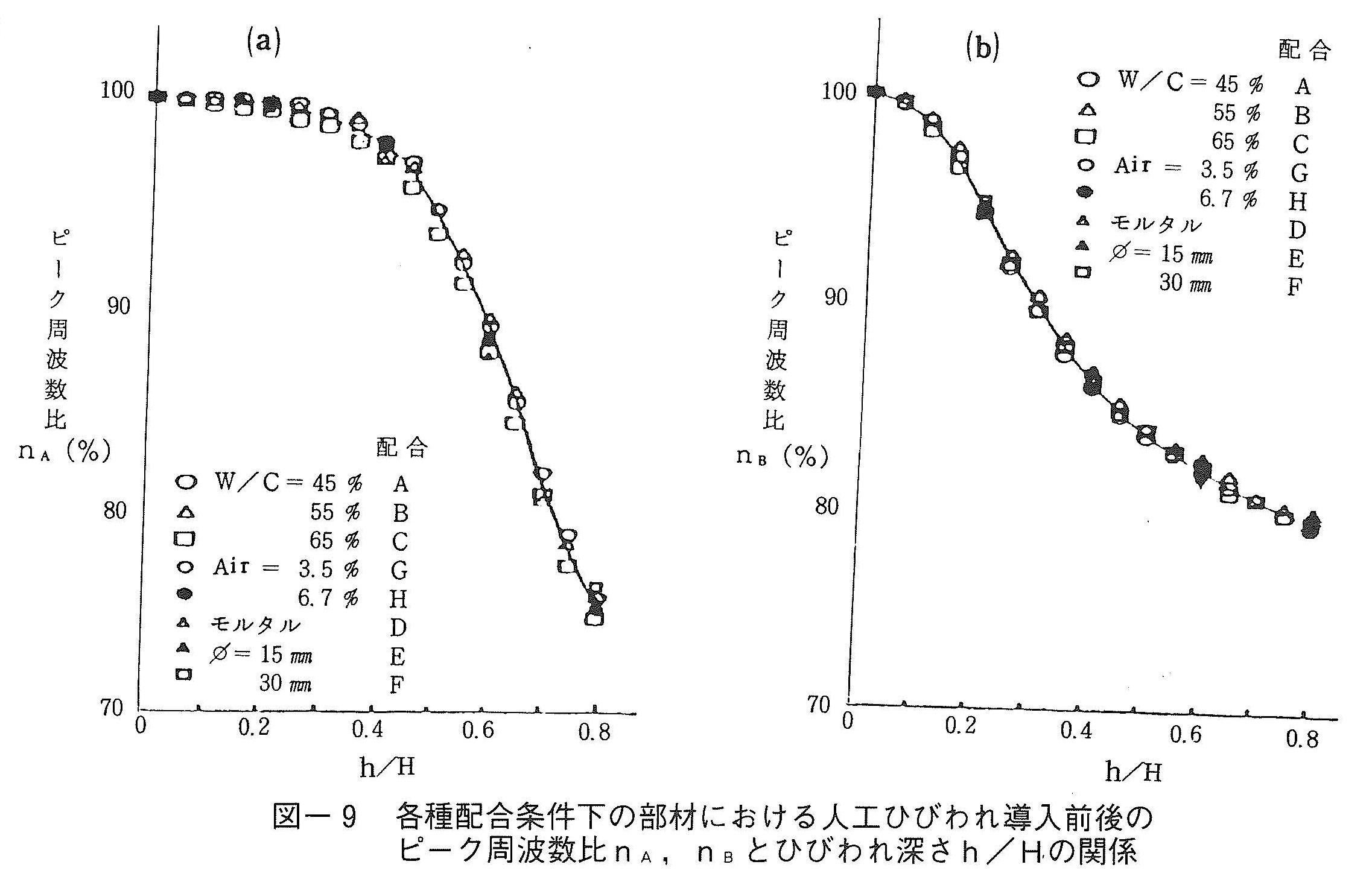
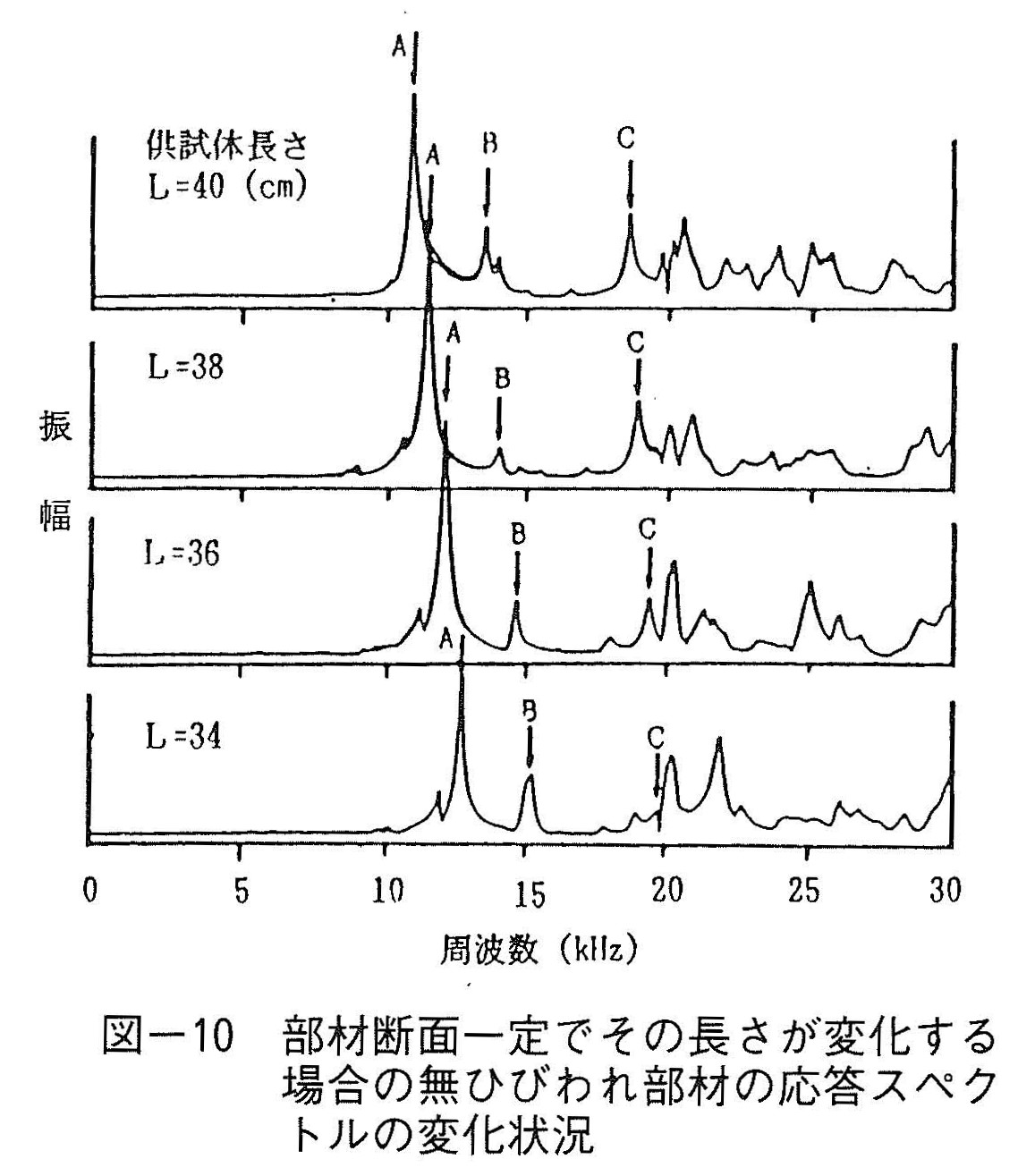
図－９は，ピークＡ，Ｂについて，ひびわれ導入前のピーク周波数ｆ_AO，ｆ_BOで，ひびわれ導入後のピーク周波数ｆ_Ah，ｆ_Bhを正規化した値ｎ_A＝ｆ_Ah／ｆ_AO，ｎ_B＝ｆ_Bh／ｆ_BOに対する，ひびわれ深さｈと部材高さHの比h／Hとの関係を示したものである。これより，ピーク周波数比ｎ_A，ｎ_Bを用いれば，どのような配合の場合においてもほぼ１つの曲線で示されることが判る。これは，これらのピークがひびわれを含む部材内部の幾何形状と，そこを伝播する超音波の伝播速度に基づく共振現象によって生じているためと考えられる。また図－10は，部材断面一定でその長さＬが34cmから40cmまで変化する場合の，無ひびわれ部材の応答スペクトルの変化状況を示している。部材長さが短くなるに従ってピークＡ，Ｂ，Ｃが漸次高周波数側へ移動する様子が判る。これより，同一コンクリートで造った供試体でも，部材形状寸法が異なれば応答スペクトル上のピーク周波数も異なってくることが判る。

その後の研究の結果，より低い周波数領域にひびわれ深さ評価に関して有効ないくつかのピークが存在することが判った^3）。そこで計測システムを改良して低周波数領域での感度を上げ，無筋および鉄筋コンクリート部材の曲げひびわれ深さ評価を試みた。ここでは従来使用していたＡＥセンサを使用せず，発信側には普通の超音波音速計用の圧電素子トランスデューサを，また受信側では圧電加速度計を使用し，ひびわれ導入前後の応答スペクトルを測定した。図－11はここで使用した人工ひびわれを有する鉄筋および無筋コンクリート部材の形状寸法，および発信，受信センサ取り付け位置を示している。曲げひびわれは，無筋コンクリート部材については外部から圧縮強度の約1／3～1／4程度のプレストレスを作用させた後，単純梁の状態で曲げ試験を行って導入した。また鉄筋コンクリート部材については，鉄筋の配置してある側のかぶりコンクリートを幅約1.2mmのカッターにて切り欠いた後単純梁の状態で同様に曲げ試験を行って導入した。そして，これを約4kg／cm²の圧力容器中で着色液に24時間浸した後取り出してひびわれ位置で割裂し，その断面の着色状況より曲げひびわれ深さを測定した。なお着色液にはビンゾール原液を水で約３倍に薄めた溶液を使用した。

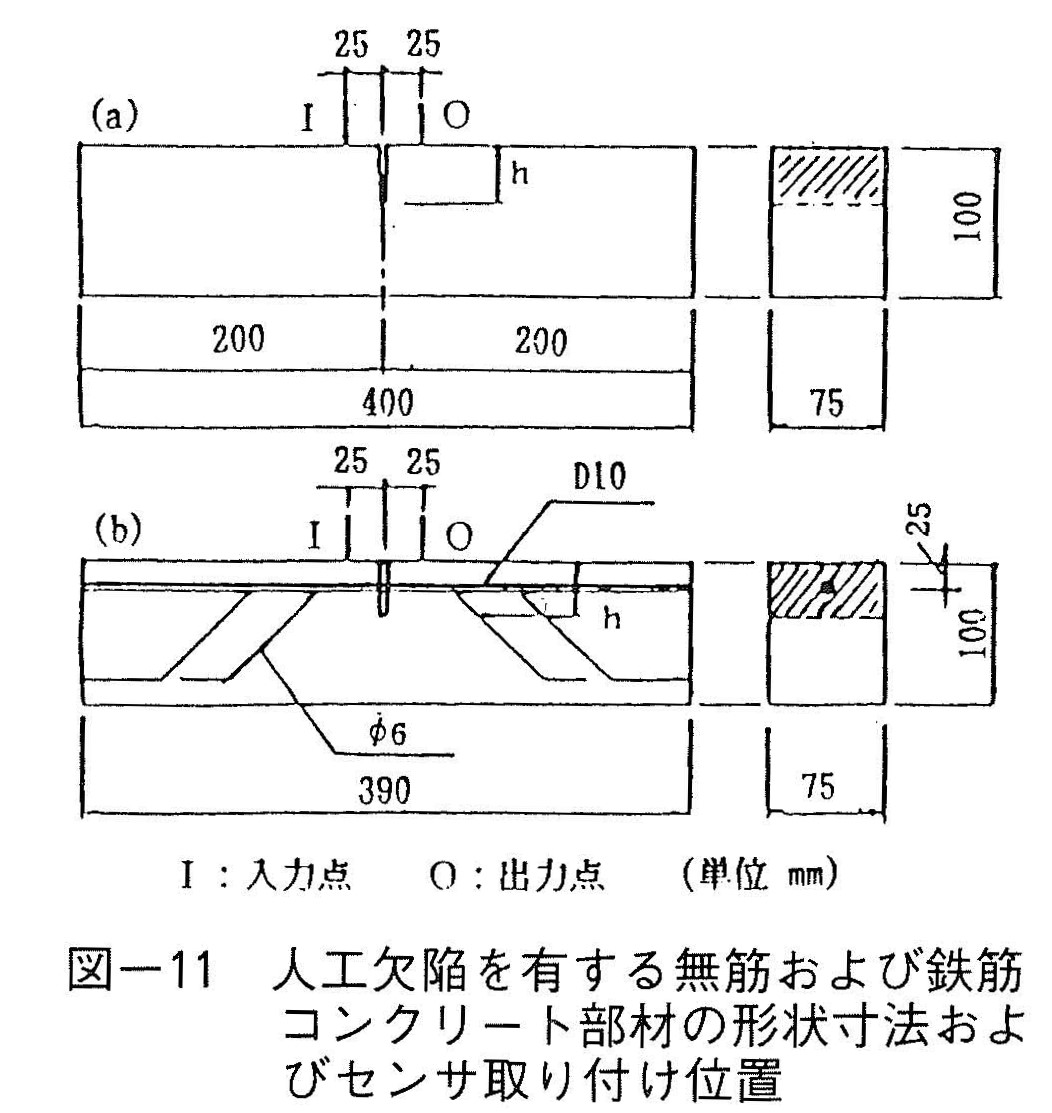
図－12は，人工ひびわれを有する無筋コンクリート部材のひびわれ深さの増加に伴う応答スペクトルの変化状況を示している。図中に矢印で示すピークＡ，Ｂ，Ｃはここで着目したピークであり，鉄筋コンクリート部材においてもほぼ同じ周波数帯域で同じようにピークが発生し，またひびわれ深さの増加に伴ってほぼ同様に低周波数側へ移動することが判った。

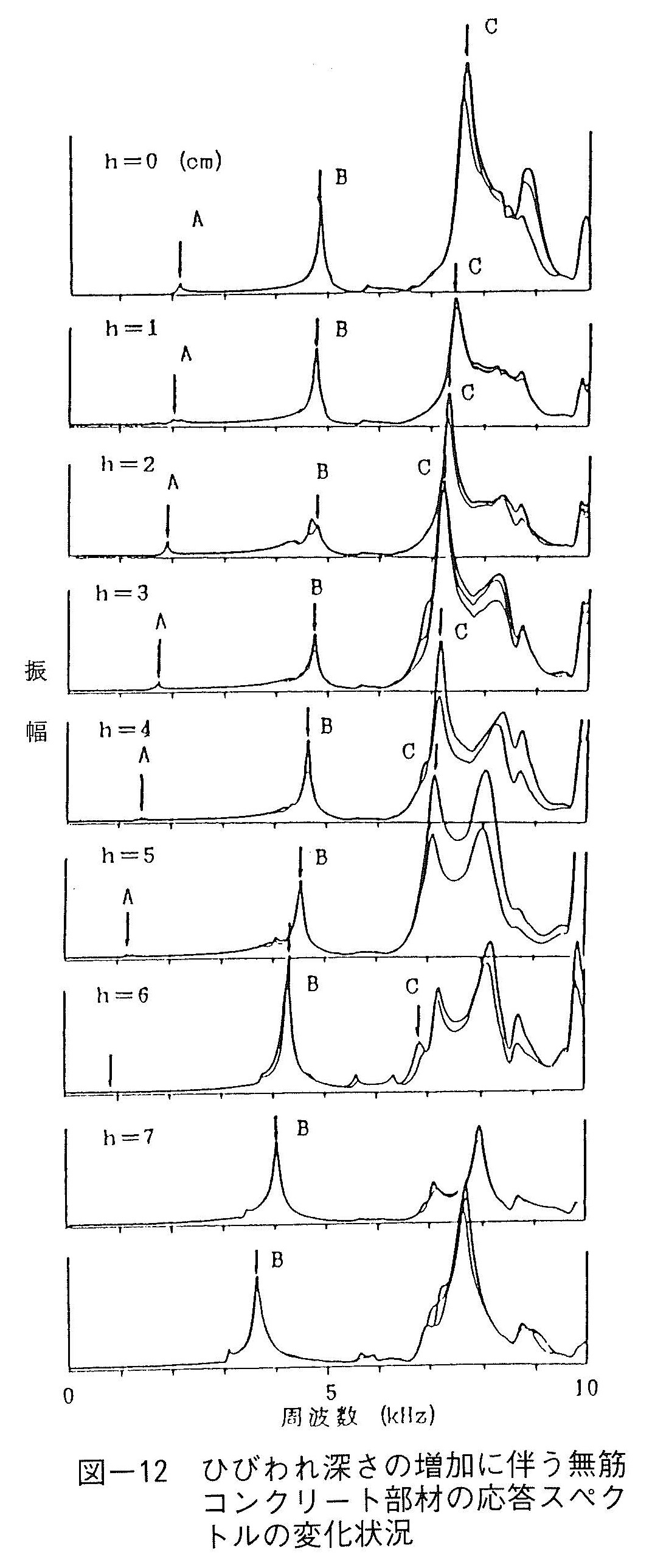
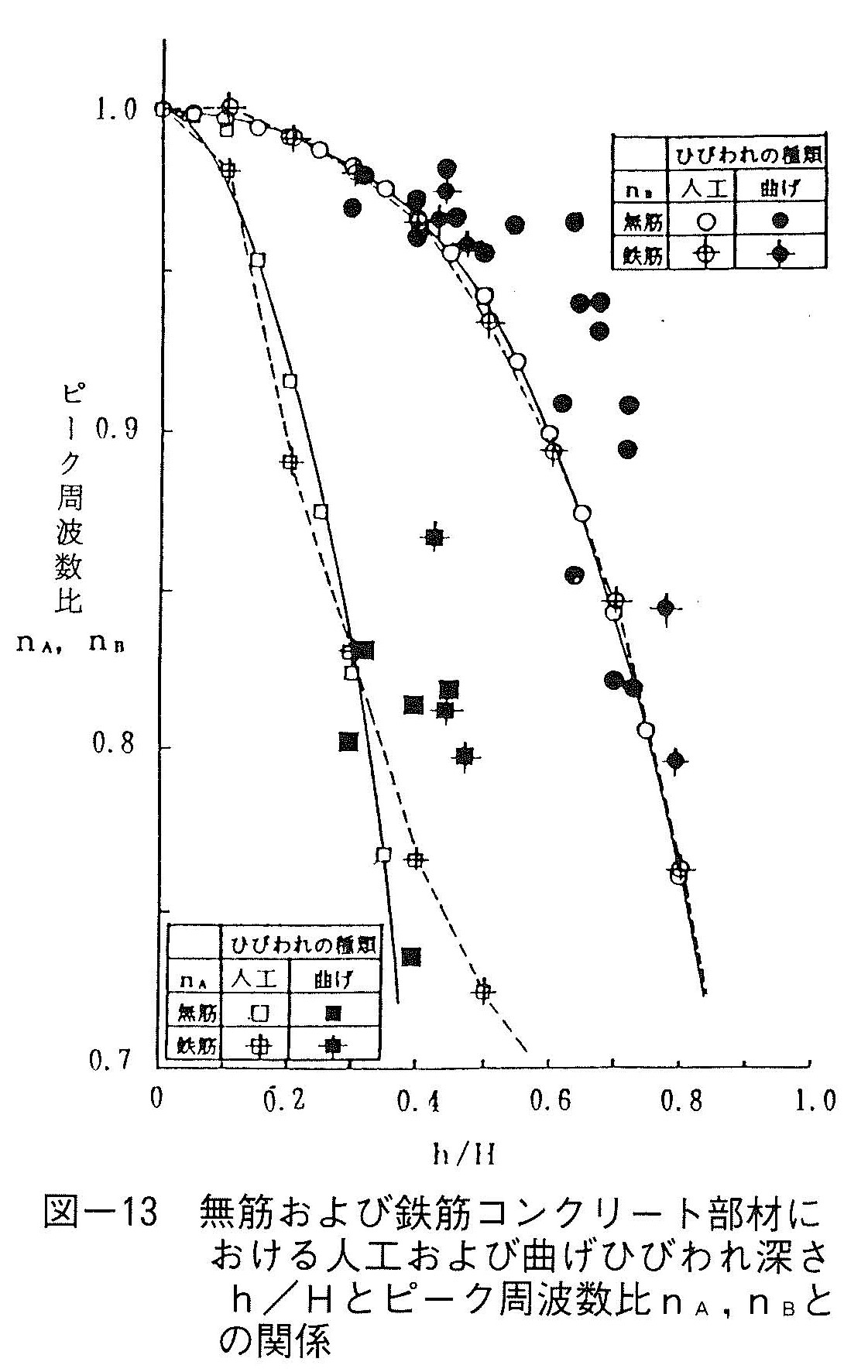
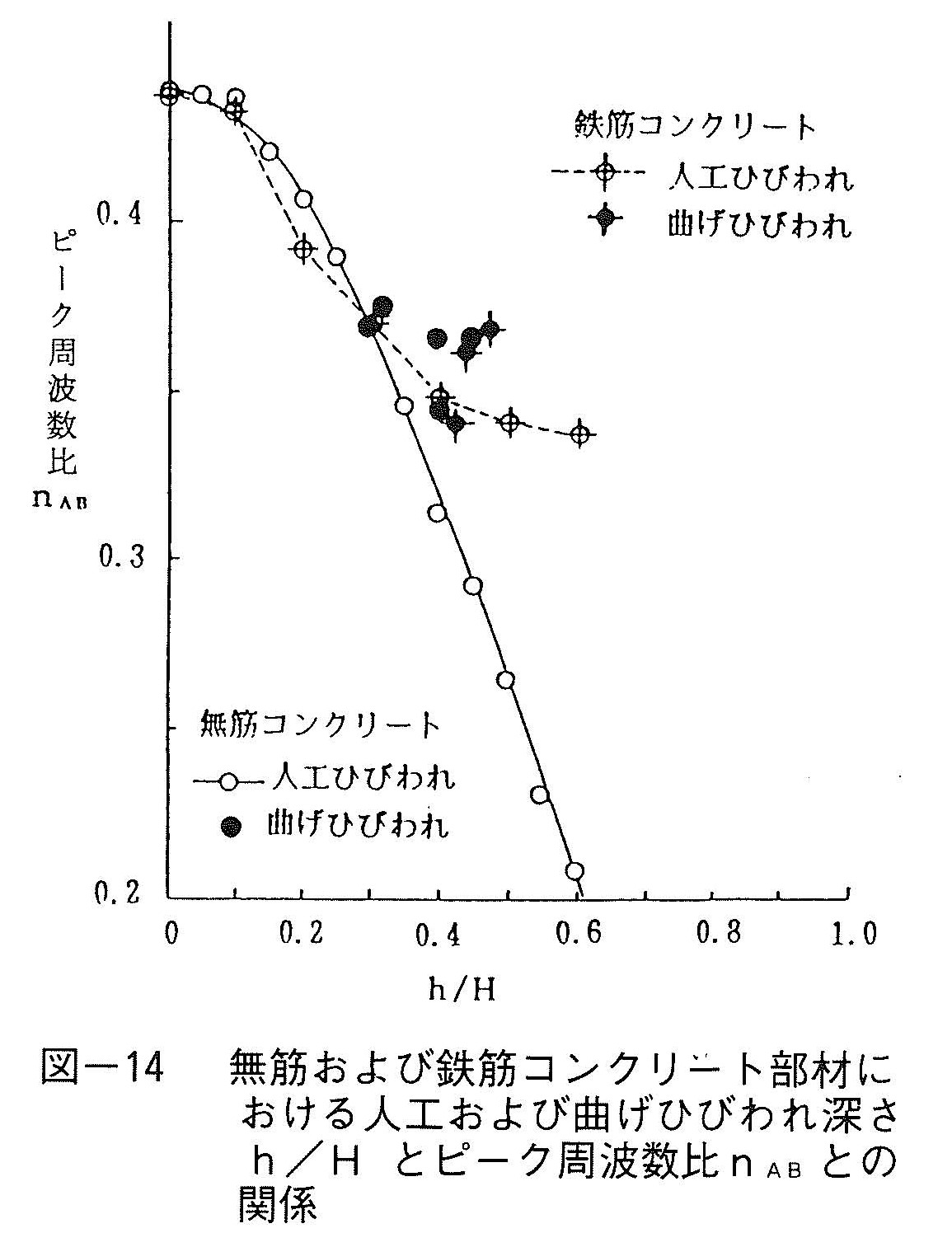
図－13は，人工ひびわれを持つ無筋および鉄筋コンクリート部材におけるピーク周波数ｎ_A，ｎ_Bとひびわれ深さh／Hとの関係を求めると共に，曲げひびわれの測定結果を併記したものである。これより，若干のばらつきはあるものの，無筋および鉄筋コンクリート部材の曲げひびわれ深さの測定結果はほぼ参照曲線の近傍にあり，本方法を用いて曲げひびわれ深さ評価が可能であることが判る。このピーク周波数比ｎ_A，ｎ_Bを用いてひびわれ深さを評価する場合，ひびわれ導入前の応答スペクトルが無ければひびわれ深さ評価は不可能である。そこでひびわれ導入後の応答スペクトルのみでひびわれ深さ評価が可能となる方法について検討した。図－14は，任意のひびわれ深さｈにおける応答スペクトル上の2つのピークAとBの周波数比ｎ_{A B} ＝ｆ_Ah／ｆ_Bhとひびわれ深さh／Hとの関係を示している。ここでも曲げひびわれ深さの測定結果はほぼ曲線の周囲にあることが判る。これより，ひびわれ導入前の応答スペクトルが有る無しにかかわらず，本方法を用いて曲げひびわれ深さ評価が可能であることが判る。

コンクリート構造物中の欠陥評価では種々のケースについて検討したが，ここでは無筋および鉄筋コンクリート部分からなる壁状構造物模型中の欠陥評価と，ＰＣ桁中のグラウト充填度評価について述べる。

図－15は実験に使用した人工欠陥を有する壁状構造物模型の形状寸法並びに欠陥配置状況を示している。この構造物模型中には発泡スチロール製の板状欠陥とポーラスコンクリートの蜂の巣状欠陥を無筋および鉄筋コンクリートの板状部分にそれぞれ埋設すると共に，無筋コンクリート部分に深さの異なる2つの表面開口ひびわれを設けた。板状欠陥の寸法は一辺20cm，厚さ約２cmの角形欠陥であり，無筋および鉄筋コンクリート部分にそれぞれ深さを違えてコンクリート表面に平行に埋設した。蜂の巣状欠陥（30×40×10cm）は無筋および鉄筋コンクリート部分の板厚中央部にそれぞれ１個ずつ埋め込んだ。応答スペクトルの測定では発信および受信センサ間隔を５cmとして両センサを同一表面に取り付けて行う表面法と，欠陥部の表裏両面に取り付けて行う透過法を使用した。

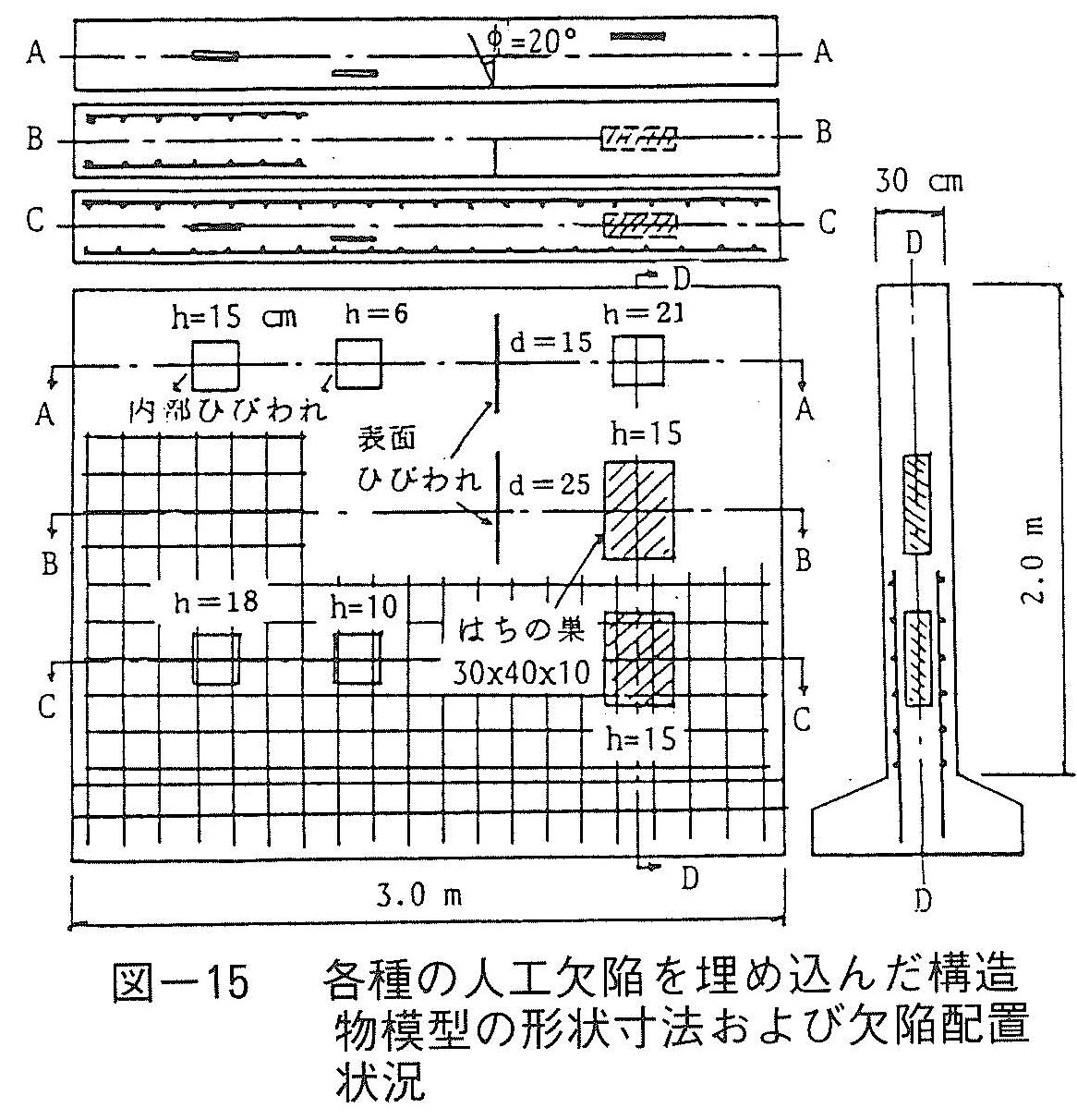
図－16，17は壁状構造物の各欠陥部および無欠陥部を表面法と透過法で得られた応答スペクトルを示している。表面法では，無筋および鉄筋コンクリート部共に無欠陥部の応答スペクトル上には約５kHz以下にはほとんど顕著なピークが見られないのに比べて，無筋コンクリート部の板状欠陥が浅い場合（ｈ＝６cm）には約３kHz付近に振幅の大きなピークが現われ，また中程度の深さ（ｈ＝15cm）においても約4.3KHz付近に明瞭なピークが現れているのが判る。また鉄筋コンクリート部の欠陥深さｈ＝10cmにおいても同様に約3.9kHz付近に顕著なピークが出現している。しかしながら，欠陥が深くなると顕著なピークは見られず，識別し難くなっている。蜂の巣状欠陥がある場合には，無筋および鉄筋コンクリート部共に無欠陥部に比べて約５～７kHz付近に凹凸の激しいイレギュラーな応答が見られ，何か異常性を感じさせる結果となっている。表面ひびわれ部においては全体的に凹凸の激しい応答が見られ，異常性が感じられる結果となっているが，ひびわれ深さを判定できるまでには至っていない。透過法では受信センサに欠陥が近い方を浅い方とした。透過法では，無筋および鉄筋コンクリート部共に欠陥が浅い場合および中程度の場合にそれぞれ表面法とほぼ同じ周波数帯域に顕著なピークが見られ，また透過法では欠陥が深い場合においても顕著なピークが現れているのか判る。これより，本方法では透過法の方がより深い欠陥まで識別出来ることが判る。

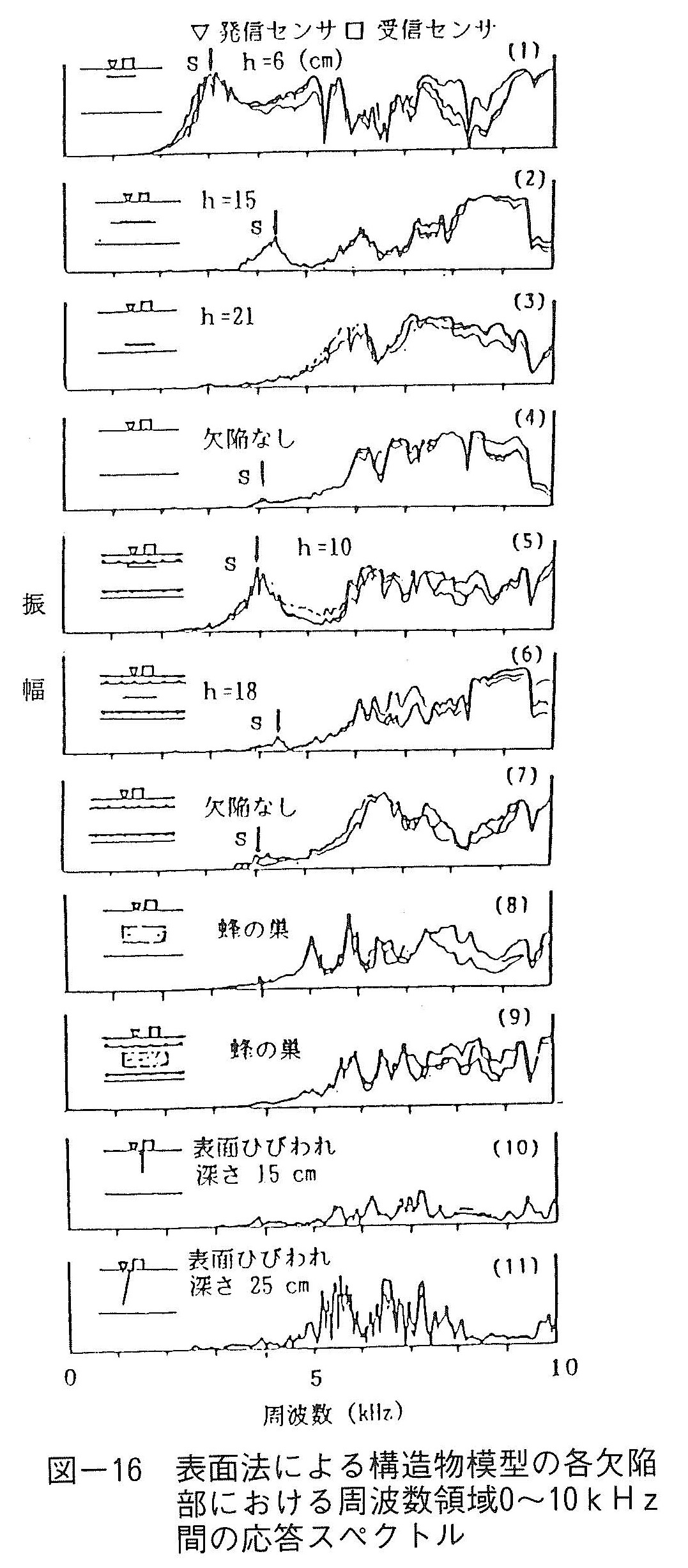
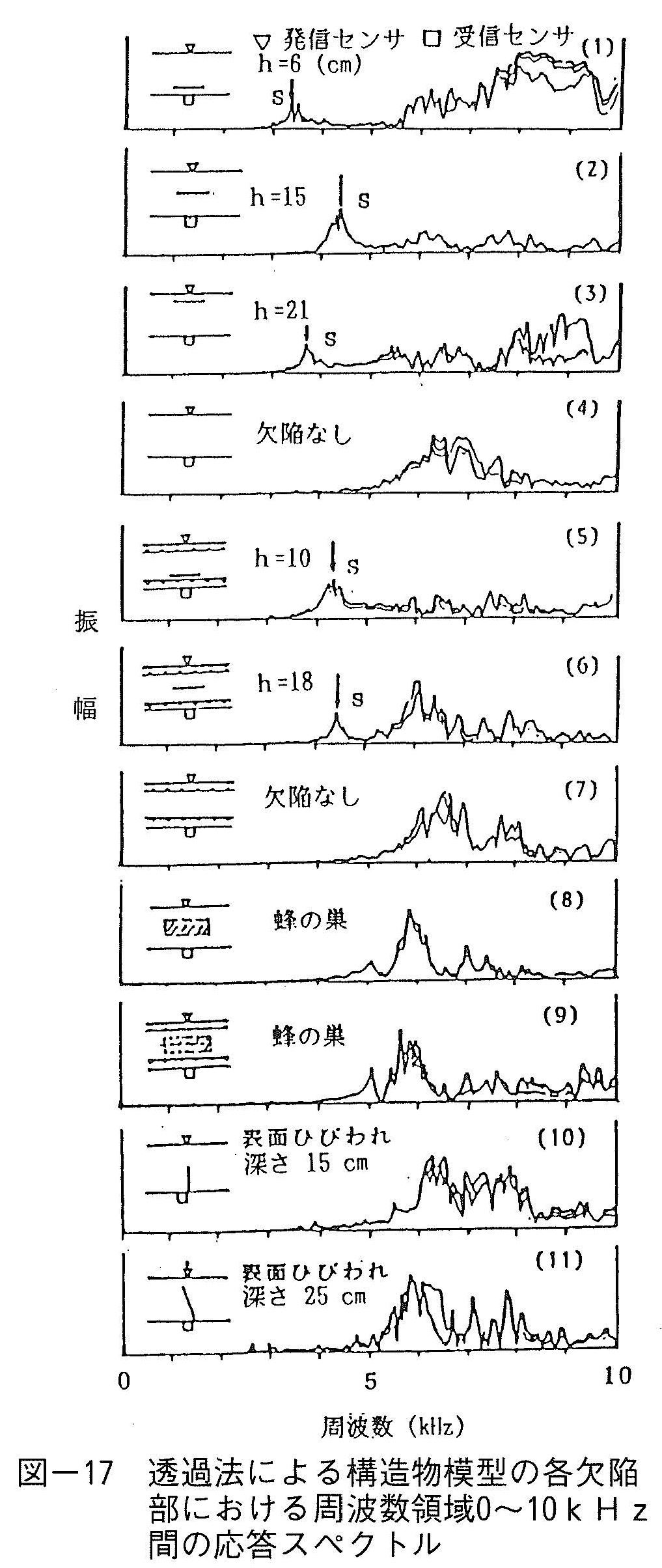
図－18は，橋梁架設現場にてグラウト充填度評価の実験に使用したポストテンションＰＣ桁の形状寸法および測点配置状況を示している。グラウト充填度評価は，架設前のＰＣ桁に対して，午前中にグラウト充填前の応答スペクトルをシース軸線上で測定した後，午後からその桁に対してグラウト充填を施し，翌日の午前中に同じ位置でのグラウト充填後の応答スペクトルを測定した。応答スペクトルは主に表面法で測定し，一部で透過法でも測定した。

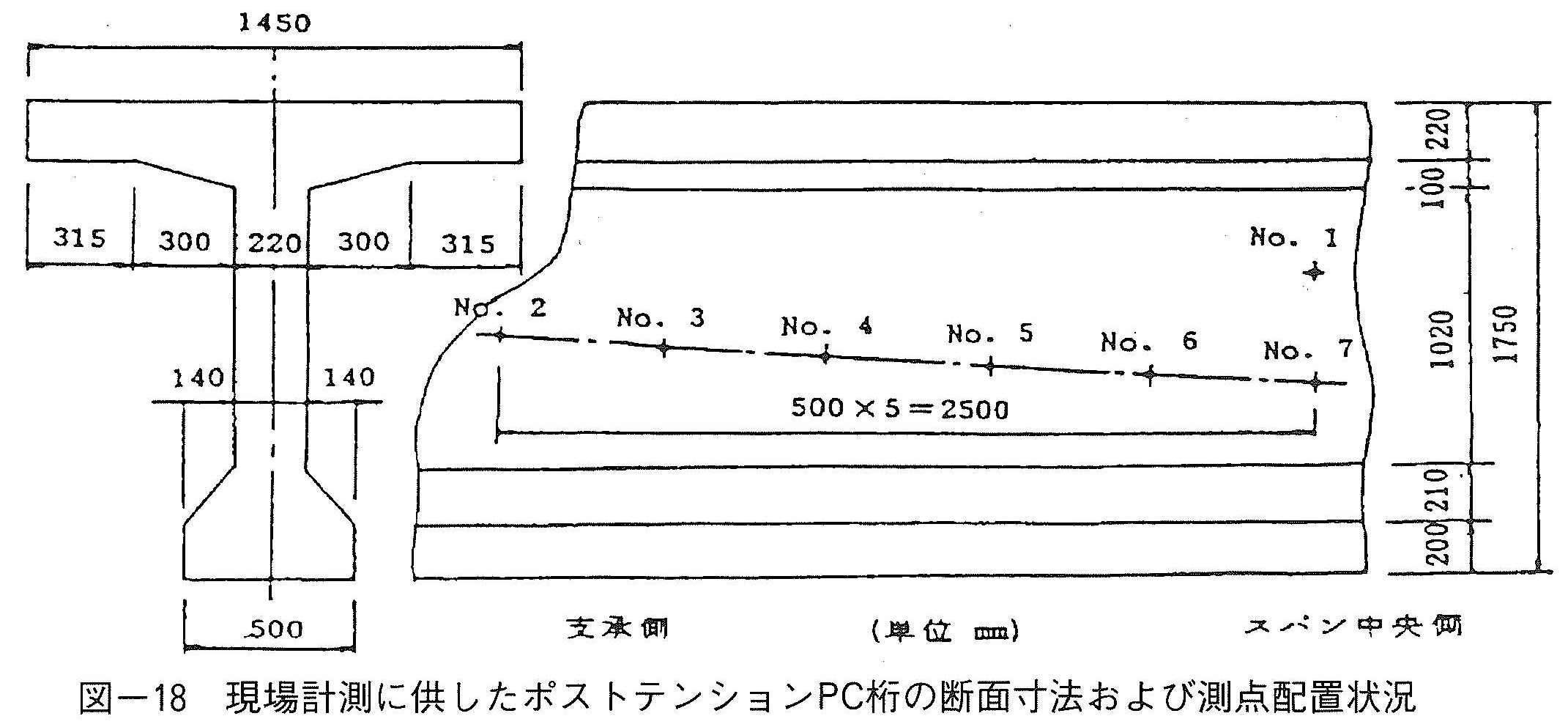
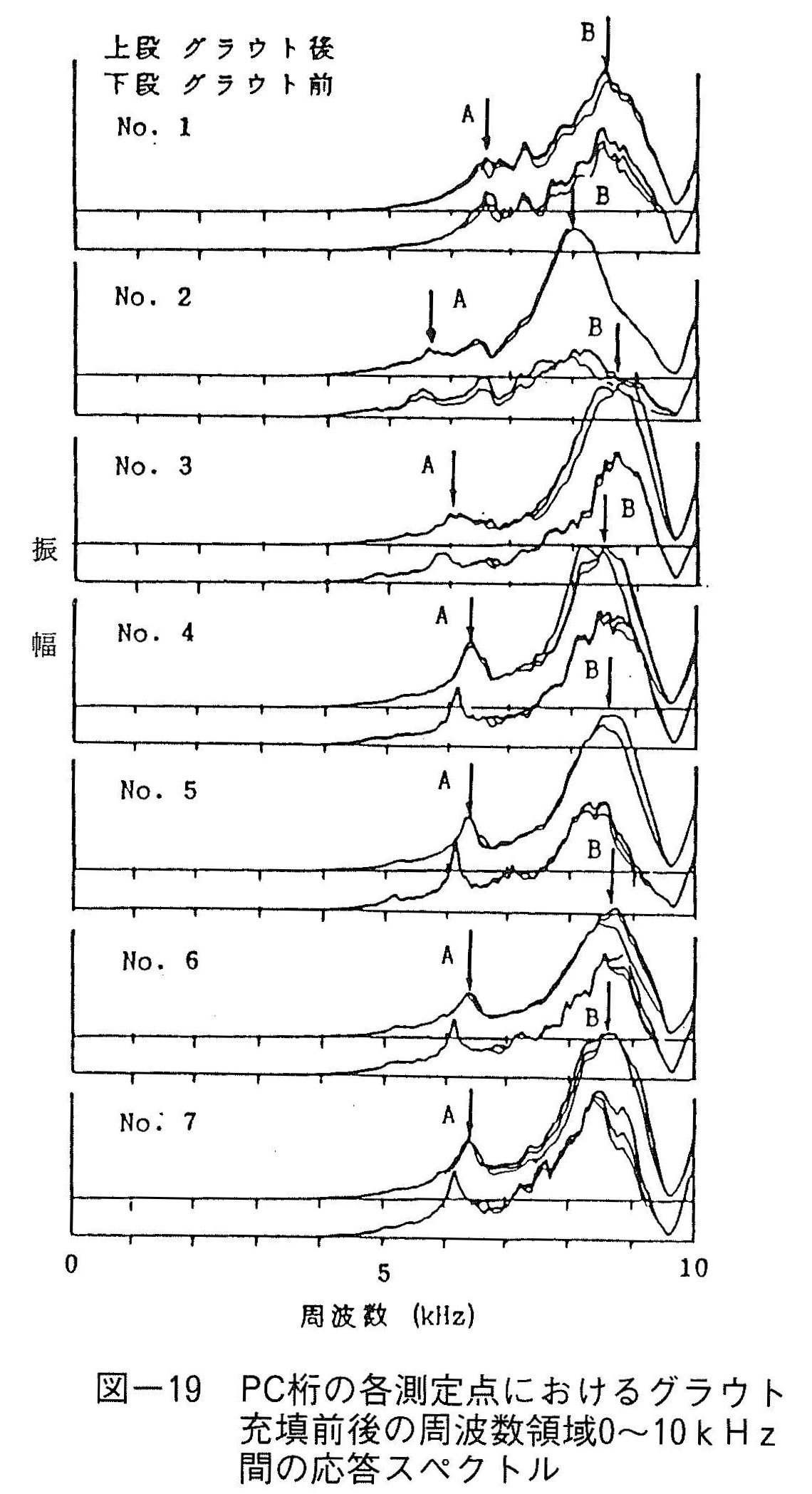
図－19はＰＣ桁のグラウト充填前後における応答スペクトルの変化状況を示している。全般的に類似したパターンの応答が見られ，比較的滑らかな応答の中に，約６kHz付近と8.5kHz付近に顕著な２つのピークＡ，Ｂが出現している様子が判る。そしてそれらのピークはダクトが無い部分（No.１）ではグラウト充填前後においてピーク周波数にほとんど変化が見られないのに比べて，シース軸線上ではグラウト充填前後でピーク周波数に若干の相違が生じている様子が判る。これらのピークのうち，ピークＢはピーク先端が比較的丸みを帯びているためグラウト充填前後におけるピーク周波数の相違が判り難いが，ピークＡは尖鋭であり，グラウト充填後におけるピーク周波数の相違が明瞭に識別できる。また，測点No.７においては透過法も試みたが，表面法同様にピークＡにおいてグラウト充填前後のピーク周波数に明瞭な相違が見られた。これより，本方法を用いてこのようなＰＣ構造物におけるグラウト充填度評価が可能であると考えられる。なお，これらの実験結果に基づく応答スペクトルの変化状況は，境界要素法による２次元共振解析によって理論的に確認されている^5）。

以上の結果を要約すると次のような結論が得られる。

１）スィープモード入力による応答スペクトルとフーリェスペクトルとは等価である。

２）応答スペクトル上の初期ピーク周波数は共振法縦振動法における一次共振周波数に等価である。それ故，本方法を用いてコンクリートの材料的性質の推定や凍結融解過程におけるコンクリートの劣化度評価が可能である。

３）本方法を用いて形状寸法一定の無筋および鉄筋コンクリート部材の曲げひびわれ深さをおおよそ評価できる。この場合，ひびわれ導入前後の応答スペクトル上の同一ピークの周波数比を用いれば，配合条件の相違に基づく音速の影響を無視出来る。

４）本方法を用いて無筋および鉄筋コンクリート構造物中の扁平な欠陥や蜂の巣などの内部欠陥の存在をおおよそ評価出来る。またポストテンションＰＣ構造物中のダクト内のグラウト充填度評価がほぼ可能である。

最後に，本報告は超音波スペクトロスコピー法によるコンクリート中の欠陥評価に関するこれまでの一連の研究成果を限られた紙面の中で大幅に要約して述べたので，少なからず判り難いものとなったことをお詫び申し上げます。詳細については参考文献をご参照下さるようお願い申し上げます。