汎用ソフトを用いた硬岩NATMのための観察情報の数値化
大分工業高等専門学校土木工学科
助教授
助教授
相 川 明
九州大学工学部建設都市工学科
教授
教授
樗 木 武
1 はじめに
NATMは,吹付コンクリート,鋼製支保工,ロックボルト等の支保部材を用いて,地山の耐力を活用するトンネル工法であり,広く用いられている。しかしながら,わが国の地山は複雑であり,同一トンネルでも断面ごとに支持能力に差がある場合が多く,地山の状況に応じて,数種類の支保パターンを採用しているのが一般的である。そのために,図ー1に示すように,事前調査をもとに支保パターンの概略を決定した上で,施工時には,計測管理により,適切な設計内容に修正しながら掘進する方法が採用されている1)2)。
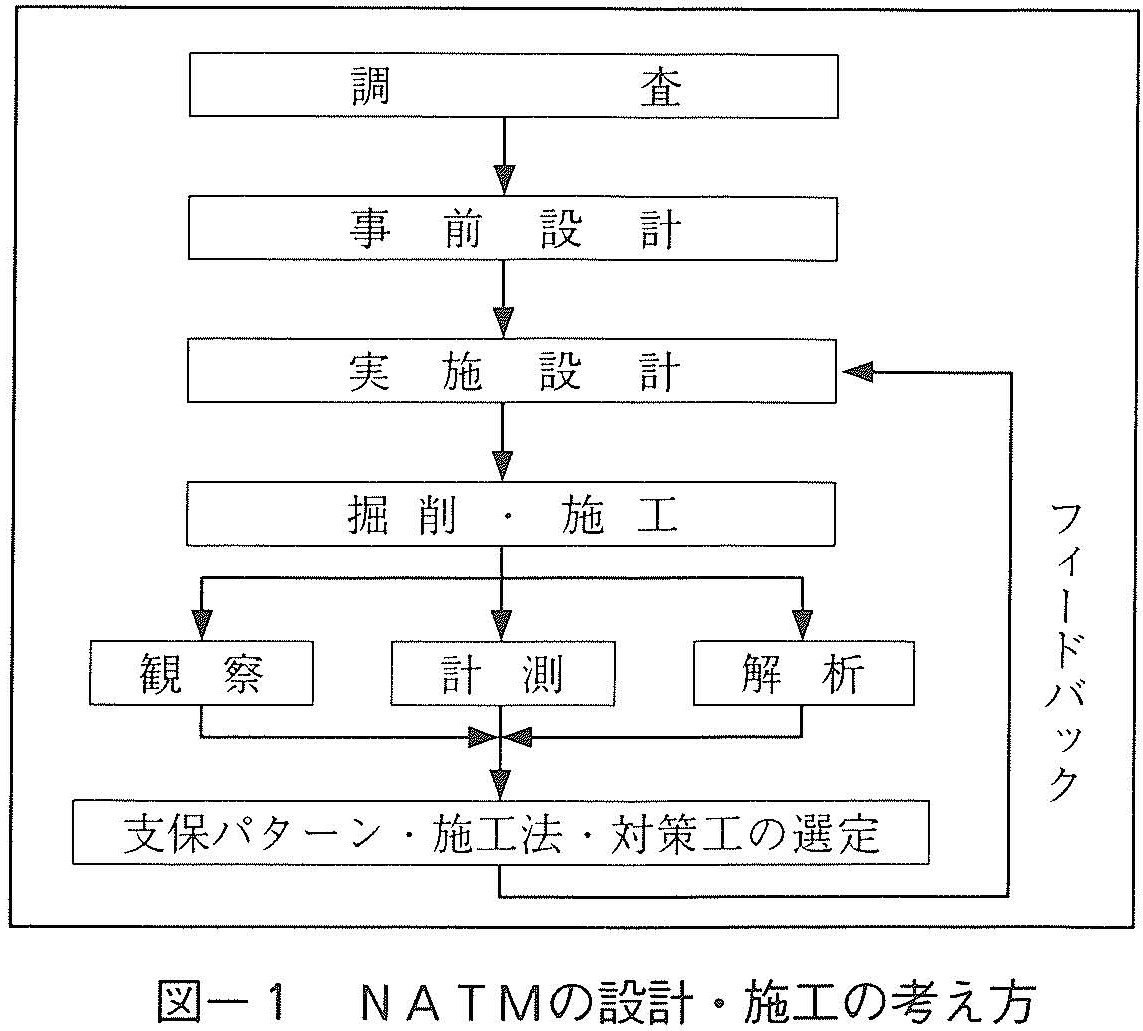
ところが,表ー1に示すように,たとえば硬岩地山では,地山の変形量が小さく,計測に関して十分な精度を確保しにくいことから,施工時の支保パターンに関する判断は,切羽観察などによる技術者の経験と勘に依存する面が多いようである。

切羽観察は即時的に得られ,地山の状況を把握するには有効であるが,他方,数値的に表現できないため客観的な利用が遅れている分野でもある。
従来より,観察情報を施工管理に利用する研究がなされているが3)-9),実施工に応用するには,現場独自のデータを収集・整理して,誰かが統計解析を行わねばならず,しかも,プログラミングに関する知識が必要であり,多くの仕事を処理しなければならない第一線の技術者にとっては,これらのことが隘路となっていた。
最近では解析ソフトの発達により,手法については概略を理解するだけでも,解析が行える状況になりつつある。本報告は観察結果を数値化する方法について概説するものであるが,著者らは,表計算ソフトLotus1-2-3上でデータベース構築から,解析,作図,印刷までの一連の作業が行える多変量解析ソフトを用いた。10)11)
2 観察に基づく施工管理モデルの構造
(1)線形モデル
トンネルの安定性は,地山と支保との相互作用によって達成される。これらの挙動を表現する物理モデルが明らかであれば,支保の施工内容を容易に決定できるはずであるが,まだ未解明な点が多い。そこで,数学モデルの構築手法を応用して,物理モデルに近い関数形を推定することを考える。数量化理論などの,いわゆる線形モデルでは,これらの複雑な関数を次のような一次式で近似する。

上式は,要因1~要因nからなる要因の重ね合わせでyが決まることを意味する。yを目的関数,要因のことを説明変数という。たとえば,支保パターンが,土被り,断面積,岩種,亀裂,湧水の5つで決まると考えると,次のような関数となる。

物理モデルでなければ意味がないという考え方もあるが,トンネルー地山の連成挙動に関する支配方程式を,説明変数についてテイラー展開すると一次式に帰着するので,その関数形がこれと類似のものとなることを想定するものである。なお係数は実データに基づいて決定されるが,決定方法により,各種のモデル構築法が存在する。
(2)目的関数の設定
施工管理モデルは,本来は,物理モデルをもとに構築する必要があることは明白であるが,トンネルー地山系の支配方程式に施工時の地山情報をそのまま入力することは困難であり,現状では,力学モデルの構造を無視したまま,説明変数と目的関数の因果関係のみに依存してモデル構築することが多い。そのため,地山条件が異なると説明力を失うなどの問題が発生しがちである。以下にこれらの問題が起きないようにするための工夫について述べる。
線形モデルは非常にシンプルなものであるこれが力学的に意味を持つ関数とするためには,説明変数の選択と目的関数の設定に関して何らかの仕掛けが必要である。すなわち,モデルの形状を決めるにあたり,支保のメカニズムと観察結果とを適切に関連づけることが重要である。
NATMの主要な支保部材は,吹付けコンクリート,鋼製支保工,ロックボルトであるが,観察を定量化する研究の多くは,これらの支保部材の組み合わせである標準支保パターンを,切羽観察を説明変数として,直接判別する方法を採用している(図ー2左)。また,複数のパターンの類型化では,いくつかの関数軸を用いるが,一般には解析過程をブラックボックスとして扱っているので,それらの関数形は,いわばデータのばらつきのみに依存して勝手に決まり,解析者が当初予定したようには判別できない。
目的関数が「穏やか」とか「やすらぎ」などのような形容詞的なものの場合には,直接判別する方法が有効であるが,支保パターンのように明らかに支保効果に序列があり,しかもその序列の間隔が不明なものを識別する場合には,見かけ上の精度の向上のみを求めず,客観的な物理量として評価できるものを目関係数に採用すべきであると考える。例えば複数の関数軸に異なる力学的な意味を与えて,施工中に得られる情報を一旦これらの関数軸に凝縮した上で,次に関数軸と支保パターンとの関連性を考慮すれば,トンネルの挙動に対応する的確な判断を得られ,また信頼性の把握や代替案の設定も容易になる。ここでは,図ー2右のように,数値的な表現が可能な吹付けコンクリートと鋼製支保工の仕様を目的関数とし,さらに,支保パターンと関連づけることにする。
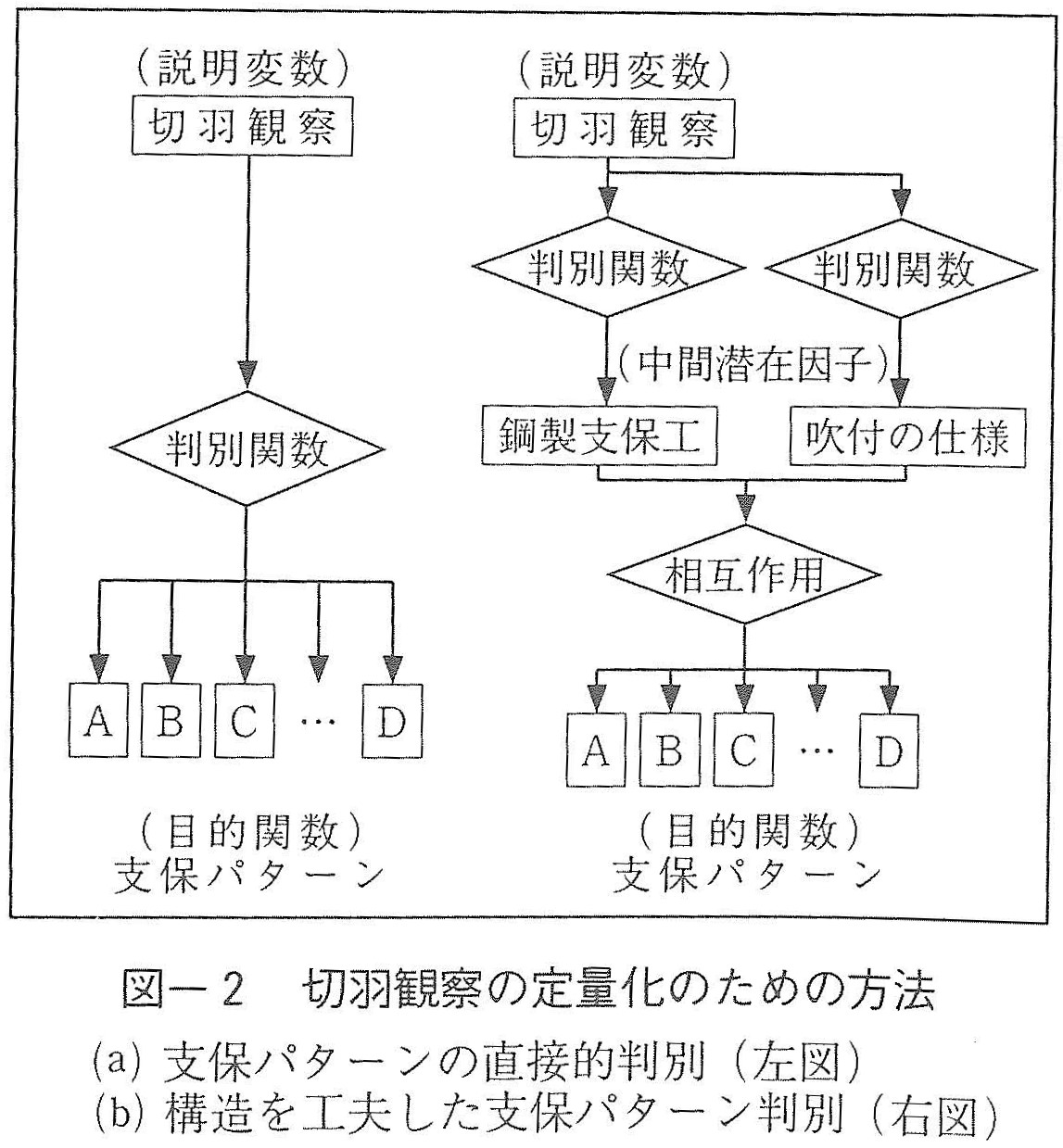
(3)説明変数の選定
説明変数に関しては,たとえば以下のような項目が要求される。
① 判別モデルが力学的な裏付けを持つために,説明変数は荷重・地山の変形特性・トンネル形状や大きさを代表する変量であること。
② 操作性がよいこと。すなわち,比較的簡単な調査のみで容易に入手でき,しかもできる限り客観的・定量的評価が可能なものであること。
③ モデルの適用にあたり,説明変数は施工内容との関連が大きいもので,できるだけ互いに独立で相互補完的な因子であること。しかも,目的関数との相関関係が,現実面と符号上の矛盾を生じないものであること。
④ 頑健で汎用性のあるモデルとするために,説明変数の数は最小限にとどめること。
3 施工時の支保パターンの変更状況
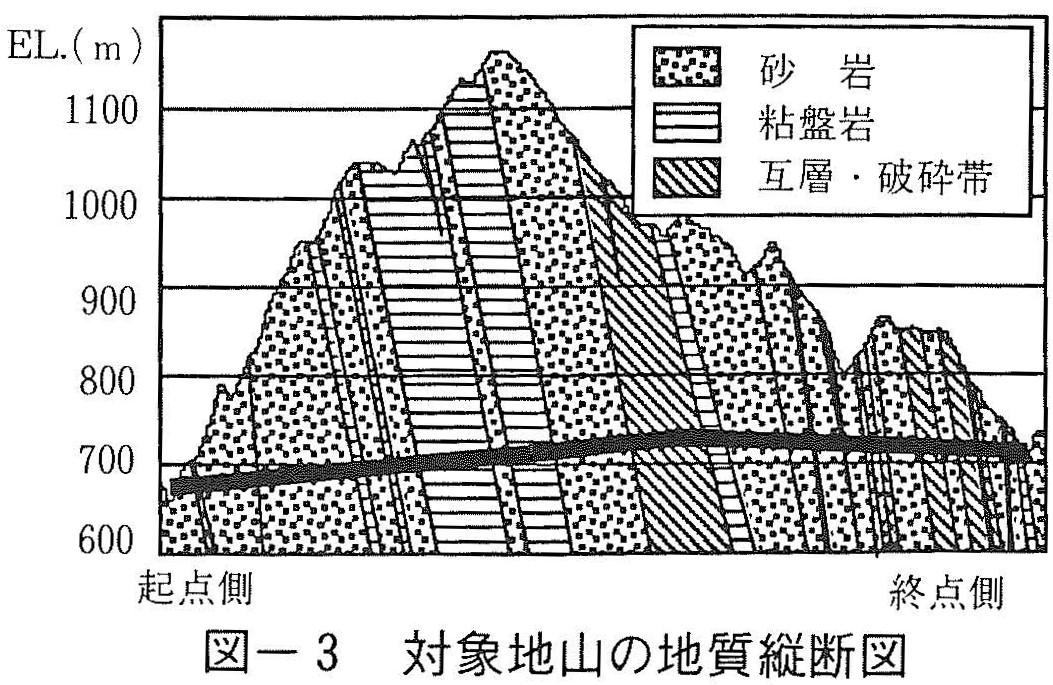
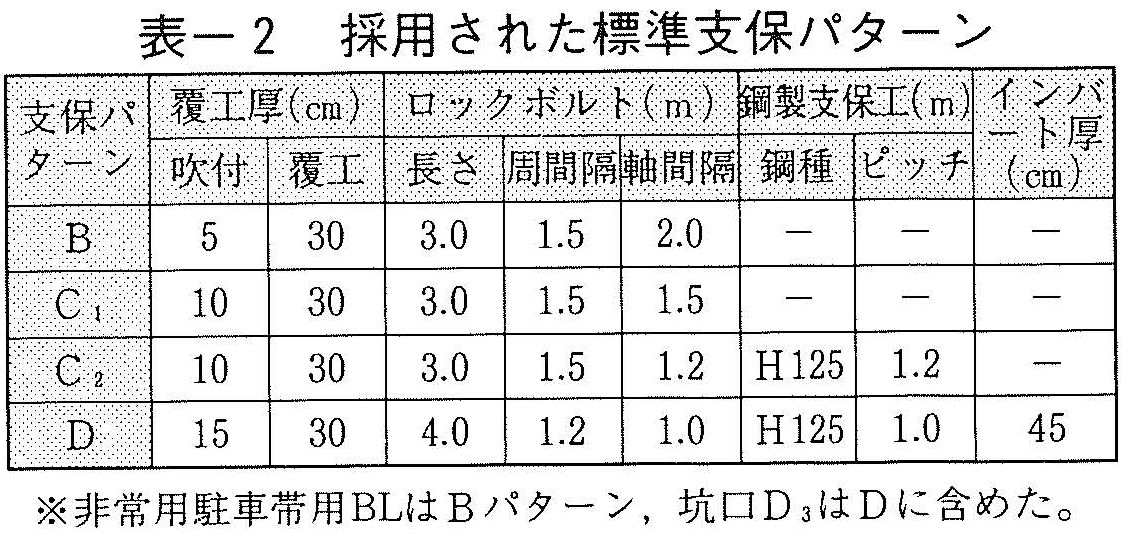
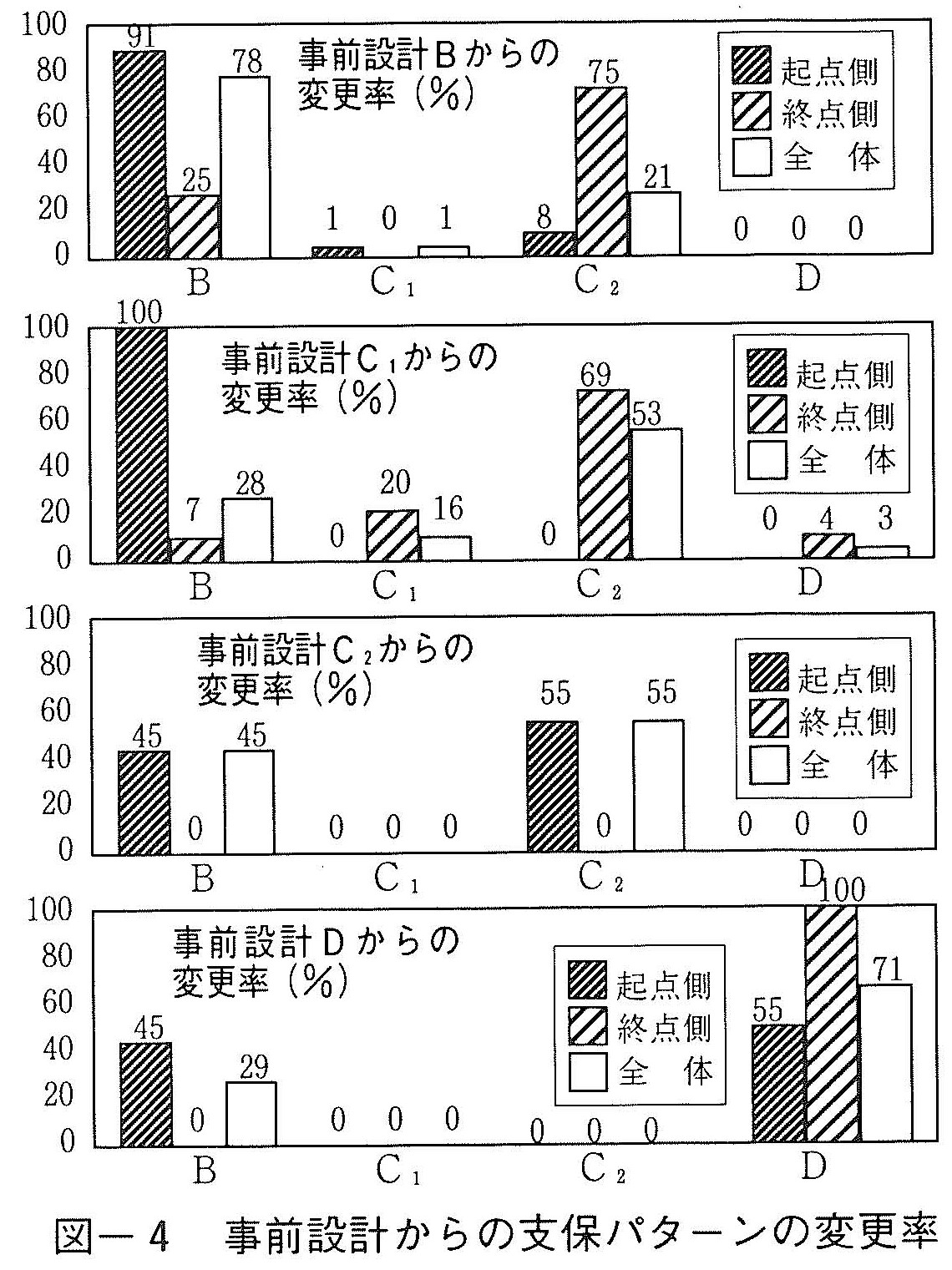
解析例のトンネル縦断図を図ー3に示す。これは,砂岩,粘板岩主体の中古生層に施工された延長約2,800m,最大土被り450mの2車線道路トンネルである。事前設計は道路トンネルの標準設計法によった。標準支保パターンを表ー2に示す。本トンネルは起点側と終点側の2工区に分けて,両坑ロより施工され,データ入手時の掘進長はそれぞれ約1,100m,400mである。施工実績ではこれらの延長のうち,起点側の18%,終点側の70%,全体の32%の断面で支保パターンが変更されている。
図ー4に事前設計からの支保パターンの変更率を示す。起点側では,支保のランクに関して,上位側への変更が目立つ。逆に終点側では,下位側への変更が多い。全体では2ランク以上の変更も多く,事前設計の信頼性は必ずしも十分とはいえないことが指摘できる。
4 目的関数と説明変数
(1)目的関数の設定
目的関数の標準支保パターンと,本解析で考慮する鋼製支保工の有無と吹付けコンクリート厚との関係を示すと表ー3のようになる。モデルの構築は,これら2つの目的関数について別々に行う。

(2)説明変数の選択
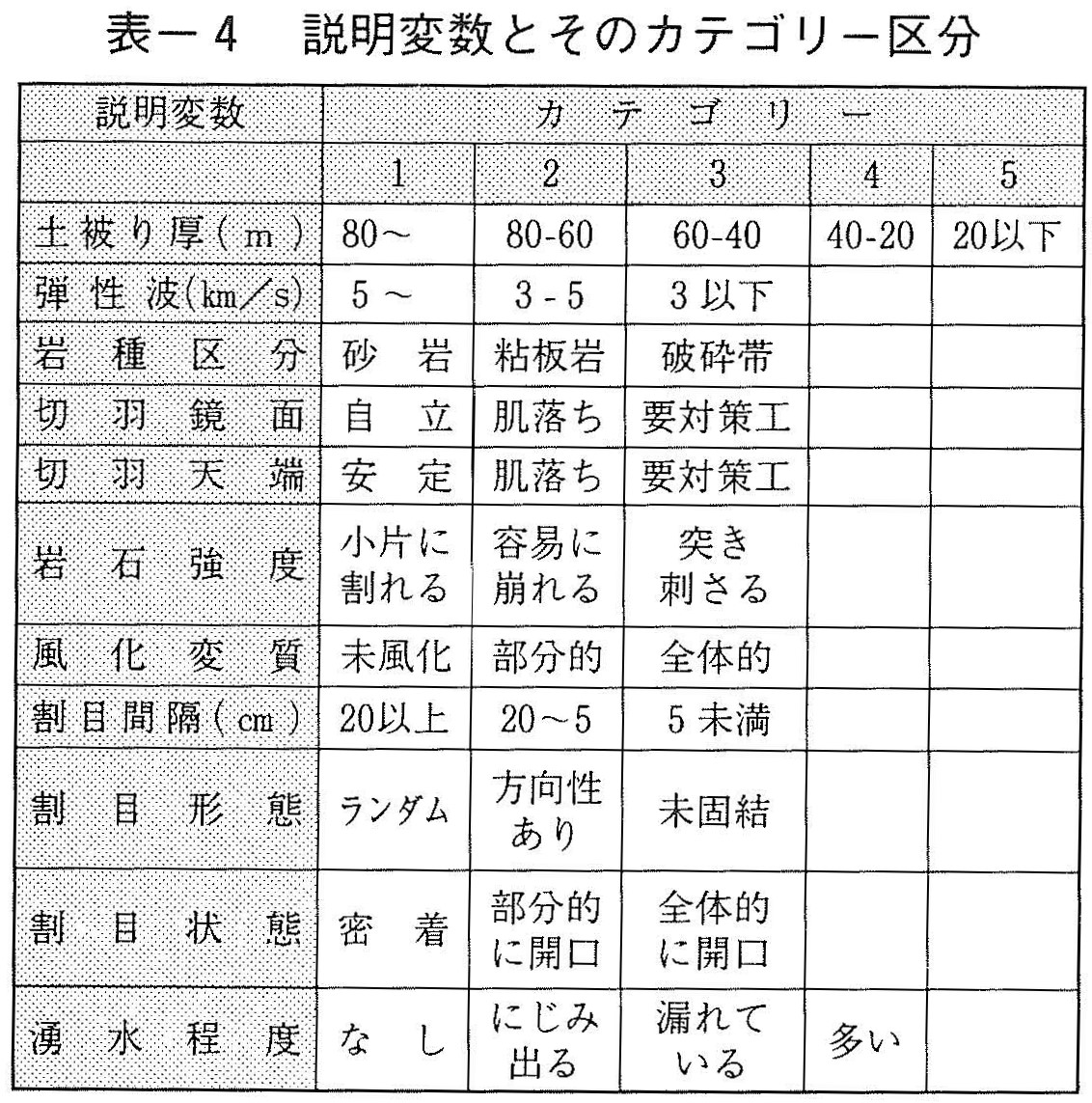
切羽観察シートをもとに,観察8項目を抽出し,出現頻度を考慮して表ー4のように簡略化した。表では,切羽観察項目のほかに,土被り,弾性波速度,岩種区分を含めているが,これらはトンネル周辺の比較的広い範囲での地山の力学的な条件を考慮するためである。
5 解析結果とモデルの比較
(1)支保パターンの直接的な判別モデル
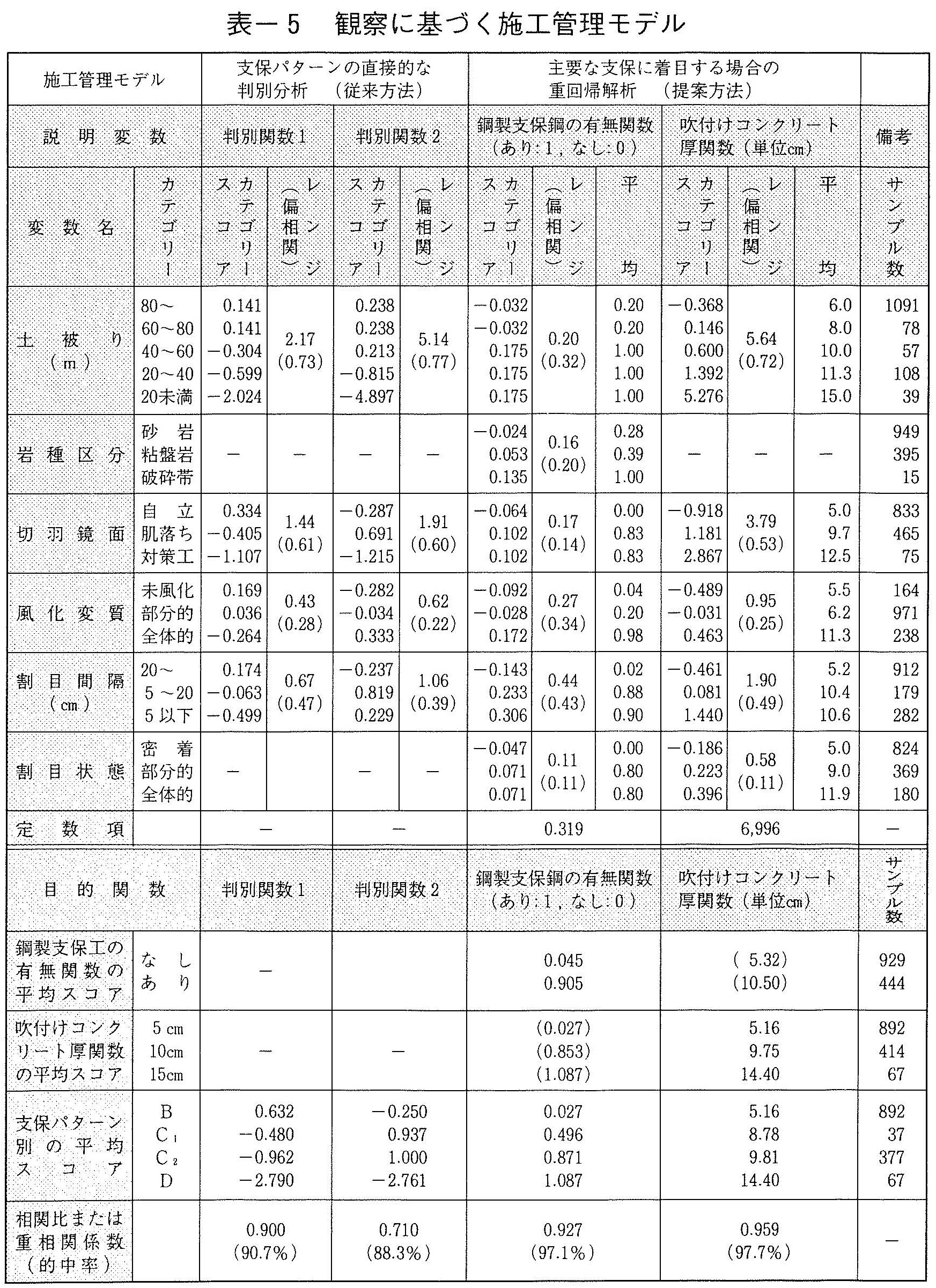
これら説明変数をもとに,支保パターンを数量化理論2類で直接判別した「従来方法」と,鋼製支保工の有無と吹付けコンクリート厚を目的関数として,数最化理論1類による重回帰分析を行った「提案方法」の結果を表ー5に示す。
従来方法では,相関比が大きい判別関数2つについて示す。以下,これらを判別関数1,判別関数2とする。施工パターンの判別は,表に示す各項目について観察を行い,該当するカテゴリースコアを足しあわせ,合計値がいずれのパターンの平均値に近いかによって判断する。本モデルの説明力の良否は相関比で判断でき,相関比が1に近いほど実際をうまく再現していることを意味する本モデルでは第1軸で0.900,第2軸で0.710であり,相関比の上では良好なモデルといえる。
つぎに,説明変数と施工パターンの関連性について検討しよう。説明変数はすべての変数が判別に大きく関与しているわけでなく,説明変数の有効性は,レンジ幅および偏相関係数により判断できる。また,説明変数のカテゴリースコアの正負の傾向を調べることにより,変数が現実にあうようにモデルに関与しているか,あるいは,矛盾を生じているかがわかる。たとえば,割目の間隔では,間隔が小さくなるほど地山の条件が厳しくなるので,より丈夫な施工パターンのスコアに近くなるべきであろう。表では,割目の間隔が小さくなるに従って,および,施工パターンがB,C1,C2,Dと頑丈になるにしたがって,カテゴリースコアが負から正へと変わっており,一般的な判断と一致し,有効な変数といえる。本表では,偏相関係数およびレンジ幅が小さく判別に寄与しないもの,あるいは,カテゴリースコアの符号に現実と矛盾するものについては除外した。表より,判別分析に有効な変数は,土被り,切羽鏡面,風化変質,割目間隔の4つである。
(2)主要な支保に着目した判別モデル
提案方法では,鋼製支保工に関する関数は,鋼製支保工の必要性を0~1の数値で出力する。数値が大きい方が鋼製支保工の必要性が高い。対象地山での支保の理論値は,反応したカテゴリースコアを加えあわせ,さらに定数項を加えて得られる。一方,吹き付けコンクリートに関する関数は,吹付コンクリートの厚さを数値(cm)で出力する。
以下これらを「鋼製支保工の有無関数」および「吹付けコンクリート厚関数」とよぶ。モデルの的中率は,鋼製支保工の有無関数が97.1%,吹付けコンクリート厚関数が97.7%と非常に良好である。
つぎに,説明変数と施工パターンの関連性について検討してみる。ここに挙げた説明変数については,カテゴリースコアの増減の傾向と,目的関数の平均スコアの傾向とはいずれも矛盾を生じず,一般的な現象に一致している。また,レンジ幅,および偏相関係数でモデルヘの寄与の大きさを比較すると,土被り,岩種区分,切羽鏡面,風化変質,割目間隔,割目状態の変数が有効であった。
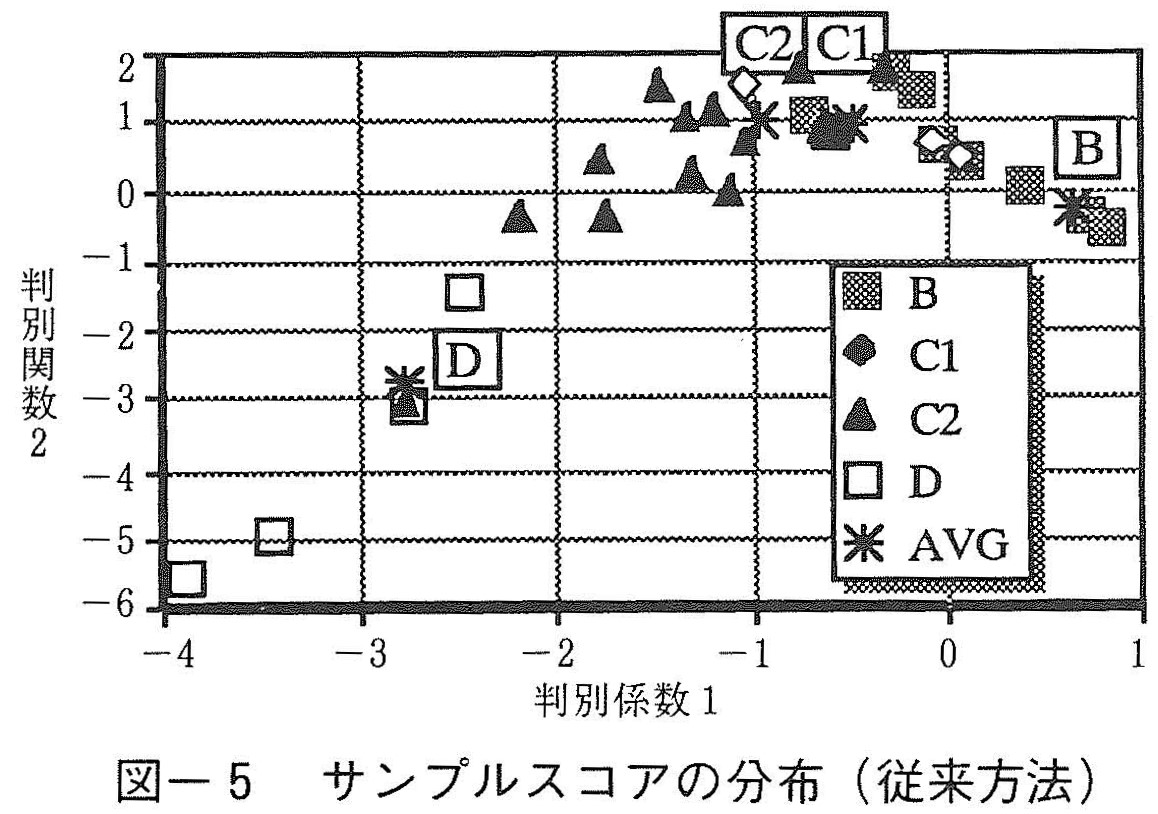
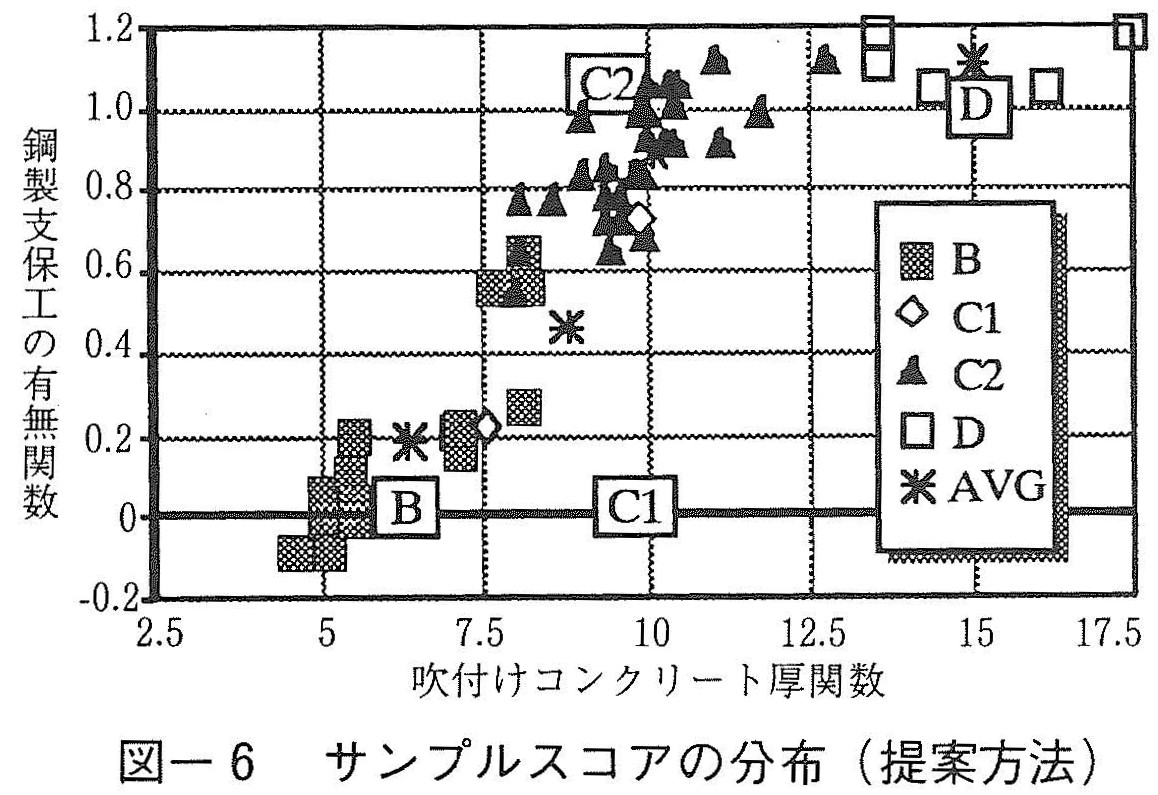
(3)サンプルスコアの分布図
図ー5および図ー6に両モデルのサンプルスコアの分布図を示す。図より各支保パターンの施工内容の差異が二次元平面上の距離で視覚的に把握できる。図中の*印は各支保パターンの平均値である。ある地山データが与えられると,それがいずれの支保パターンに近いかにより,どの支保パターンを採用したらよいかを判断できるはずである。図ー5では,判別関数1は,B,C1,C2,Dの支保パターンを序列化するが,判別関数2の意味は不明瞭であり,数値がいかなる物理量と関連するものか明らかでない。したがって,従来の方法では,施工内容をどのように変更すればよいかという具体的な判断を得難い。このように支保パターンを直接的に判別する方法では,判別関数軸の意味があいまいであることが,判断を困難にしているといえる。
一方,提案方法は,鋼製支保工の有無関数が0で,吹付けコンクリート厚関数が5の点がBパターンであり,吹付けコンクリート厚関数が10の点がC1パターンとなる。また鋼製支保工の有無関数が1で,吹付けコンクリート厚関数が10の点がC2パターンであり,吹付けコンクリート厚関数が15の点がDパターンとなる。判別関数軸の意味が明確であり,各支保パターンも明瞭に判別されている。ことに,C1パターンは採用断面数が少ないため,従来の方法では十分な判断を得られないが,提案方法によると両パターンの差異が把握できる。また,提案方法では,対象地山での最適な支保パターンが得られると同時に,施工内容をどのように変更すればよいかという方針を得ることが可能である。
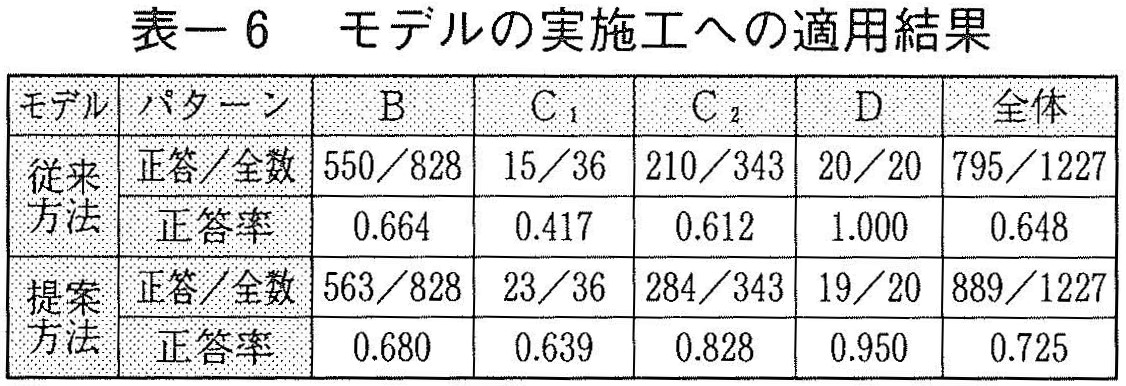
(4)モデルの実施工への適用結果
モデル構築に使用しなかったトンネル中間部のデータをもとに,掘削を再現する思考実験を行い,従来の方法と提案方法と精度を比較した。結果を表ー6に示す。表より提案方法が精度が高く,有効性が認められる。とくに,モデル構築時に採用断面数が少ないC1については,先見情報が不足し,従来方法では十分な判断結果を得られなかったが,提案モデルでは有効に機能していることがわかる。
6 おわりに
本報告は,まず,観察情報を施工管理に利用する際のモデル構築方法の考え方についてまとめ,さらに,吹付コンクリートの厚さや鋼製支保工の必要性などの「意味ある複数の物理量」と観察情報を関連づけることにより,観察情報をいくつかの関数軸に凝縮し,それらの関数値のクロスにより施工内容を決定するという方法を提案した。本法は簡単ではあるが,判断を容易にし,従来に比ベ精度を向上することができた。本解析では,計測情報については言及しなかったが,計測情報も同様に扱うことにより,施工管理の改善が期待できる。また,本法をいくつかの地山について適用することにより,評価軸が同じ意味を持つことから,地山の差異を評価にも役立てることができる。いずれにせよ,岩盤に関するメカニズムを解析の中により多く反映することが重要であると考える。
参考文献
1)日本道路協会:道路トンネル観察計測指針,p296,1993.
2)日本道路協会:道路トンネル技術基準(構造偏)同解説,pp237-243,1989.
3)土木学会:トンネルにおける調査・計測の評価と利用,pp188-267,1987.
4)日本トンネル技術協会:地山評価のあり方に関する研究,日本トンネル技術協会,p36,1985.
5)吉中龍之進,桜井春輔,菊池宏吉:岩盤分類とその適用,土木工学社,p231,1989.
6)Z.T.Bieniawski:Engineering Rock Mass Classifications,p203,1989.
7)清水則一,櫻井春輔:ファジー理論を用いた岩盤分類の構成方法に関する研究,土木学会論文集,370/3~5,pp225-232,1986
8)鈴木昌次,古川浩平,井上洋司,中川浩二:ファジィ回帰モデルに基づくトンネルの岩盤分類法の提案,土木学会論文集,418/3~13
9)荒木義則,鈴木昌次,宮崎智司,日永田雅司,古川浩平,中川浩二:ニューラルネットワークを用いた NATM施工時の支保パターン選定構造のモデル化に関する研究,土木学会論文集,522/6~28,pp143~153,1995.
10)長谷川勝也・川口輝久:Lotus1-2-3による科学技術計算フォーム集,共立出版,p160,1987.
11)Lotus1-2-3多変量解析,オードマン㈱,1991.




